
Bivariegated graph
Encyclopedia
In graph theory
, a mathematical discipline which has applications in computer science, as well as in many other disciplines, a bivariegated graph is a graph whose vertex set can be partitioned
into two equal parts such that each vertex is adjacent to exactly one vertex from the other set not containing it.
In a bivarigated graph G with 2n vertices, there exists a set of n independent edges such that no odd number of them lie on a cycle of G.
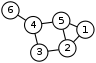
, shown below, is a bivariegated graph: if one partitions it into an outer pentagon and an inner five-point star, each vertex on one side of the partition has exactly one neighbor on the other side of the partition. More generally, the same is true for any generalized Petersen graph
formed by connecting an outer polygon and an inner star with the same number of points; for instance, this applies to the Möbius–Kantor graph
and the Desargues graph
.
Any hypercube graph, such as the four-dimensional hypercube shown below, is also bivariegated.
 However, the graph shown below is not bivariegated. Whatever you choose the three independent edges, one of them is an edge of a cycle.
However, the graph shown below is not bivariegated. Whatever you choose the three independent edges, one of them is an edge of a cycle.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a mathematical discipline which has applications in computer science, as well as in many other disciplines, a bivariegated graph is a graph whose vertex set can be partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into two equal parts such that each vertex is adjacent to exactly one vertex from the other set not containing it.
In a bivarigated graph G with 2n vertices, there exists a set of n independent edges such that no odd number of them lie on a cycle of G.
Examples
The Petersen graphPetersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, shown below, is a bivariegated graph: if one partitions it into an outer pentagon and an inner five-point star, each vertex on one side of the partition has exactly one neighbor on the other side of the partition. More generally, the same is true for any generalized Petersen graph
Generalized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
formed by connecting an outer polygon and an inner star with the same number of points; for instance, this applies to the Möbius–Kantor graph
Möbius–Kantor graph
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
and the Desargues graph
Desargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
.
Any hypercube graph, such as the four-dimensional hypercube shown below, is also bivariegated.



