Bethe-Salpeter equation
Encyclopedia
The Bethe–Salpeter equation, named after Hans Bethe
and Edwin Salpeter
, describes the bound state
s of a two-body (particles) quantum field theoretical
system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu
, but without derivation.
Due to its generality and its application in many branches of theoretical physics, the Bethe–Salpeter equation appears in many different forms. One form, that is quite often used in high energy physics is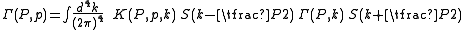
where Γ is the Bethe–Salpeter amplitude, K the interaction and S the propagator
s of the two participating particles.
In quantum theory, bound state
s are objects that live for an infinite time (otherwise they are called resonances), thus the constituents interact infinitely many times. By summing up all possible interactions, that can occur between the two constituents, infinitely many times, the Bethe–Salpeter equation is a tool to calculate properties of bound states and its solution, the Bethe–Salpeter amplitude, is a description of the bound state under consideration.
As it can be derived via identifying bound-states with poles in the S-matrix, it can be connected to the quantum theoretical description of scattering processes and Green's functions.
The Bethe–Salpeter equation is a general quantum field theoretical tool, thus applications for it can be found in any quantum field theory. Some examples are positronium
, bound state of an electron
–positron
pair, exciton
s, bound state
of an electron–hole
pair and meson
as quark
-antiquark bound-state.
Even for simple systems such as the positronium, the equation cannot be solved exactly although the equation's formulation can in principle be formulated exactly. Fortunately, a classification of the states can be achieved without the need for an exact solution. If one of the particles is significantly more mass
ive than the other, the problem is considerably simplified as one solves the Dirac equation
for the lighter particle under the external potential
of the heavier particle.
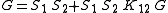
in momentum space, where "G" is the two-particle Green function
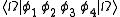, "S" are the free propagator
s and "K" is an interaction kernel, which contains all possible interaction between the two particles. The crucial step is now, to assume that bound states appear as poles in the Green function. One assumes, that two particles come together and form a bound state with mass "M", this bound state propagates freely, and then the bound state splits in its two constituents again. Therefore one introduces the Bethe-Salpeter wave function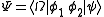
, which is a transition amplitude of two consituents 
into a bound state 
, and then makes an ansatz for the Green function in the vicinity of the pole as
,
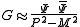where "P" is the total momentum of the system. One sees, that if for this momentum the equation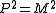
holds, what is exactly the Einstein Einstein energy-momentum relation
(with the Four-momentum
and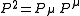 
) the four-point Green function contains a pole.
If one plugs that ansatz into the Dyson equation above, and sets the total momentum "P" such the energy-momentum relation holds, on both sides of the term a pole appears.
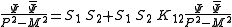
Comparing the residues yields
.
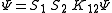This is already the Bethe–Salpeter equation, written in terms of the Bethe-Salpeter wave functions. To obtain the above form one introduces the Bethe-Salpeter amplitudes "Γ"
and gets finally
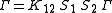
which is written down above, with the explicit momentum dependence.
, interaction is described via the exchange of particles (e.g. photon
s in quantum electrodynamics
, or gluon
s in quantum chromodynamics
), the most simple interaction is the exchange of only one of these force-particles.
As the Bethe–Salpeter equation sums up the interaction infinitely many times, the resulting Feynman graph
has the form of a ladder.
While in Quantum electrodynamics
the simplicity of the ladder approximation caused a lot of problems and thus crossed ladder terms had to be included, in Quantum chromodynamics
this approximation is used quite a lot to calculate hadron
masses, since it respects Chiral symmetry breaking
and therefore an important part of the generation these masses.
In ladder approximation the Interaction kernel does not depend on the total momentum of the Bethe-Salpeter amplitude, thus, for this case, the second term of the normalization condition vanishes.
Hans Bethe
Hans Albrecht Bethe was a German-American nuclear physicist, and Nobel laureate in physics for his work on the theory of stellar nucleosynthesis. A versatile theoretical physicist, Bethe also made important contributions to quantum electrodynamics, nuclear physics, solid-state physics and...
and Edwin Salpeter
Edwin Ernest Salpeter
Edwin Ernest Salpeter FRS was an Austrian-Australian-American astrophysicist. Born to a Jewish family, he emigrated from Austria to Australia while in his teens to escape the Nazis. He attended Sydney University, where he obtained his bachelor's degree in 1944 and his master's degree in 1945...
, describes the bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s of a two-body (particles) quantum field theoretical
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
, but without derivation.
Due to its generality and its application in many branches of theoretical physics, the Bethe–Salpeter equation appears in many different forms. One form, that is quite often used in high energy physics is
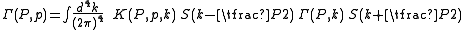
where Γ is the Bethe–Salpeter amplitude, K the interaction and S the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s of the two participating particles.
In quantum theory, bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
s are objects that live for an infinite time (otherwise they are called resonances), thus the constituents interact infinitely many times. By summing up all possible interactions, that can occur between the two constituents, infinitely many times, the Bethe–Salpeter equation is a tool to calculate properties of bound states and its solution, the Bethe–Salpeter amplitude, is a description of the bound state under consideration.
As it can be derived via identifying bound-states with poles in the S-matrix, it can be connected to the quantum theoretical description of scattering processes and Green's functions.
The Bethe–Salpeter equation is a general quantum field theoretical tool, thus applications for it can be found in any quantum field theory. Some examples are positronium
Positronium
Positronium is a system consisting of an electron and its anti-particle, a positron, bound together into an "exotic atom". Being unstable, the two particles annihilate each other to produce two gamma ray photons after an average lifetime of 125 ps or three gamma ray photons after 142 ns in...
, bound state of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
–positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
pair, exciton
Exciton
An exciton is a bound state of an electron and hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and some liquids...
s, bound state
Bound state
In physics, a bound state describes a system where a particle is subject to a potential such that the particle has a tendency to remain localised in one or more regions of space...
of an electron–hole
Electron hole
An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice...
pair and meson
Meson
In particle physics, mesons are subatomic particles composed of one quark and one antiquark, bound together by the strong interaction. Because mesons are composed of sub-particles, they have a physical size, with a radius roughly one femtometer: 10−15 m, which is about the size of a proton...
as quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
-antiquark bound-state.
Even for simple systems such as the positronium, the equation cannot be solved exactly although the equation's formulation can in principle be formulated exactly. Fortunately, a classification of the states can be achieved without the need for an exact solution. If one of the particles is significantly more mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
ive than the other, the problem is considerably simplified as one solves the Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
for the lighter particle under the external potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
of the heavier particle.
Derivation
The starting point for the derivation of the Bethe–Salpeter equation is the two-particle (or four point) Dyson equation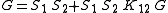in momentum space, where "G" is the two-particle Green function
Green function
Green function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
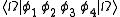, "S" are the free propagatorPropagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s and "K" is an interaction kernel, which contains all possible interaction between the two particles. The crucial step is now, to assume that bound states appear as poles in the Green function. One assumes, that two particles come together and form a bound state with mass "M", this bound state propagates freely, and then the bound state splits in its two constituents again. Therefore one introduces the Bethe-Salpeter wave function
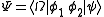, which is a transition amplitude of two consituents into a bound state , and then makes an ansatz for the Green function in the vicinity of the pole as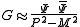 ,where "P" is the total momentum of the system. One sees, that if for this momentum the equation
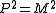holds, what is exactly the Einstein Einstein energy-momentum relationEnergy-momentum relation
In special relativity, the energy-momentum relation is a relation between the energy, momentum and the mass of a body: E^2 = m^2 c^4 + p^2 c^2 , \;where c is the speed of light, E \; is total energy, m \; is invariant mass, and p = |\vec p|\; is momentum....
(with the Four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
and 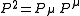) the four-point Green function contains a pole.If one plugs that ansatz into the Dyson equation above, and sets the total momentum "P" such the energy-momentum relation holds, on both sides of the term a pole appears.
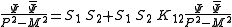
Comparing the residues yields
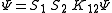.This is already the Bethe–Salpeter equation, written in terms of the Bethe-Salpeter wave functions. To obtain the above form one introduces the Bethe-Salpeter amplitudes "Γ"
and gets finally
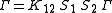
which is written down above, with the explicit momentum dependence.
Ladder Approximation
In principle the interaction kernel K contains all possible two-particle-irreducible interactions that can occur between the two constituents. Thus, in practical calculations one has to model it and only choose a subset of the interactions. As in quantum field theoriesQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, interaction is described via the exchange of particles (e.g. photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, or gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s in quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
), the most simple interaction is the exchange of only one of these force-particles.
As the Bethe–Salpeter equation sums up the interaction infinitely many times, the resulting Feynman graph
Feynman graph
A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular...
has the form of a ladder.
While in Quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
the simplicity of the ladder approximation caused a lot of problems and thus crossed ladder terms had to be included, in Quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
this approximation is used quite a lot to calculate hadron
Hadron
In particle physics, a hadron is a composite particle made of quarks held together by the strong force...
masses, since it respects Chiral symmetry breaking
Chiral symmetry breaking
In particle physics, chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of gauge theory such as Quantum Chromodynamics. The origin may be described as a fermion condensate...
and therefore an important part of the generation these masses.
Normalization
As for any homogeneous equation, the solution of the Bethe–Salpeter equation is determined only up to a numerical factor. This factor has to be specified by a certain normalization condition. For the Bethe-Salpeter amplitudes this is usually done by demanding probability conservation (similar to the normalization of the quantum mechanical Wave function), which corresponds to the equationIn ladder approximation the Interaction kernel does not depend on the total momentum of the Bethe-Salpeter amplitude, thus, for this case, the second term of the normalization condition vanishes.
Software supporting the Bethe–Salpeter equation
- YAMBO codeYAMBO codeYambo is an open source Many-body theory software package for study solids and molecular systems. It calculates the excited state properties of physical systems from first principles Yambo is an open source Many-body theory software package for study solids and molecular systems. It...
- plane wave - ExC - plane wave