
Bessel's inequality
Encyclopedia
In mathematics
, especially functional analysis
, Bessel's inequality is a statement about the coefficients of an element in a Hilbert space
in a Hilbert space
with respect to an orthonormal sequence
.
Let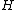 be a Hilbert space, and suppose that
be a Hilbert space, and suppose that 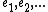 is an orthonormal sequence in
is an orthonormal sequence in 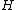 . Then, for any
. Then, for any  in
in 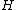 one has
one has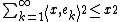
where ⟨·,·⟩ denotes the inner product
in the Hilbert space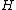 . If we define the infinite sum
. If we define the infinite sum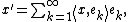
consisting of 'infinite sum' of vector resolute in direction
in direction 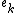 , Bessel's inequality tells us that this series
, Bessel's inequality tells us that this series
converges
. One can think of it that there exists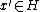 which can be described in terms of potential basis
which can be described in terms of potential basis 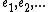 .
.
For a complete orthonormal sequence (that is, for an orthonormal sequence which is a basis
), we have Parseval's identity
, which replaces the inequality with an equality (and consequently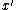 with
with  ).
).
Bessel's inequality follows from the identity: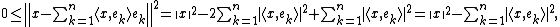
which holds for any natural n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, Bessel's inequality is a statement about the coefficients of an element
 in a Hilbert space
in a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with respect to an orthonormal sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
.
Let
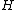 be a Hilbert space, and suppose that
be a Hilbert space, and suppose that 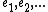 is an orthonormal sequence in
is an orthonormal sequence in 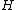 . Then, for any
. Then, for any  in
in 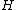 one has
one has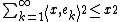
where ⟨·,·⟩ denotes the inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
in the Hilbert space
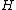 . If we define the infinite sum
. If we define the infinite sum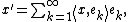
consisting of 'infinite sum' of vector resolute
 in direction
in direction 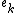 , Bessel's inequality tells us that this series
, Bessel's inequality tells us that this seriesSeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
. One can think of it that there exists
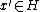 which can be described in terms of potential basis
which can be described in terms of potential basis 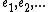 .
.For a complete orthonormal sequence (that is, for an orthonormal sequence which is a basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
), we have Parseval's identity
Parseval's identity
In mathematical analysis, Parseval's identity is a fundamental result on the summability of the Fourier series of a function. Geometrically, it is thePythagorean theorem for inner-product spaces....
, which replaces the inequality with an equality (and consequently
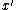 with
with  ).
).Bessel's inequality follows from the identity:
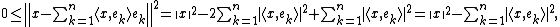
which holds for any natural n.
External links
- Bessel's Inequality the article on Bessel's Inequality on MathWorld.

