
Bayes' theorem
Encyclopedia
In probability theory
and applications, Bayes' theorem (alternatively Bayes' law or Bayes' rule) relates the conditional probabilities
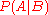 and
and  . It is commonly used in science
. It is commonly used in science
and engineering
. The theorem is named for Thomas Bayes
.
Under the frequentist interpretation of probability, probability measures the proportion of trials in which an event occurs. Under this interpretation, Bayes' theorem is the relationship between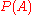 ,
, 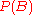 ,
, 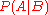 and
and  for any events
for any events  and
and  in the same event space.
in the same event space.
Under the Bayesian interpretation of probability
, probability, or confidence, measures the subjective confidence that something is true. Under this interpretation, Bayes' theorem links confidence before and after observing evidence.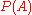 , the prior, is the initial confidence in
, the prior, is the initial confidence in  .
. 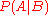 , the posterior, is the confidence having accounted for evidence
, the posterior, is the confidence having accounted for evidence  .
. 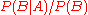 represents the degree of support
represents the degree of support  provides for
provides for  . For example, suppose somebody claims that a biased die is represented by probability model
. For example, suppose somebody claims that a biased die is represented by probability model  . The die is thrown a number of times to collect evidence,
. The die is thrown a number of times to collect evidence,  . A prior confidence of 50% may rise to a posterior of 70% if the evidence supports the model. For more detail on the application of Bayes' theorem under the Bayesian interpretation of probability, see Bayesian inference
. A prior confidence of 50% may rise to a posterior of 70% if the evidence supports the model. For more detail on the application of Bayes' theorem under the Bayesian interpretation of probability, see Bayesian inference
.
 and
and  , provided that
, provided that 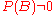 .
.
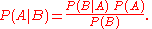
In a Bayesian inference
step, the probability of evidence is constant for all models
is constant for all models 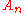 . The posterior may then be expressed as proportional
. The posterior may then be expressed as proportional
to the numerator:
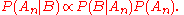
of the event space , the event space is given or conceived in terms of
, the event space is given or conceived in terms of 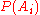 and
and  . It is then useful to eliminate
. It is then useful to eliminate  using the law of total probability
using the law of total probability
:
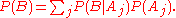

In the special case of a binary partition,
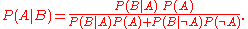
:

As previously, the law of total probability
may be substituted for unknown marginal probabilities.
 generated by two random variables
generated by two random variables  and
and  . In principle, Bayes' theorem applies to the events
. In principle, Bayes' theorem applies to the events  and
and 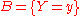 . However, terms become 0 at points where either variable has finite probability density
. However, terms become 0 at points where either variable has finite probability density
. To remain useful, Bayes' theorem may be formulated in terms of the relevant densities (see Derivation).
 is continuous and
is continuous and  is discrete,
is discrete,

If is discrete and
is discrete and  is continuous,
is continuous,

If both and
and  are continuous,
are continuous,
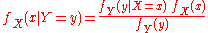
. For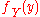 , this becomes an integral:
, this becomes an integral:
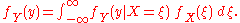
, Bayes' rule
may be thought of as Bayes' theorem in odds form
.

Where
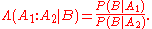
:
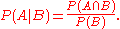
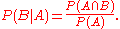
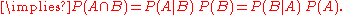

 and
and  , Bayes' theorem may be analogously derived from the definition of conditional density:
, Bayes' theorem may be analogously derived from the definition of conditional density:
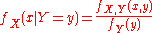
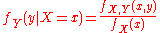
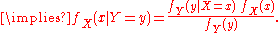
spots what might be a rare subspecies
of beetle
, due to the pattern on its back. In the rare subspecies, 98% have the pattern. In the common subspecies, 5% have a similar pattern, but he cannot distinguish these from memory. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle to be rare?
From the extended form of Bayes' theorem,
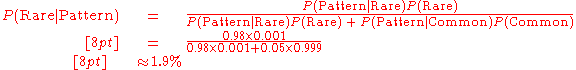
they are a user?

Despite the apparent accuracy of the test, if an individual tests positive, it is more likely that they do not use the drug than that they do!
This surprising result arises because the number of non-users is very large compared to the number of users, such that the number of false positives (0.995%) outweighs the number of true positives (0.495%). To use concrete numbers, if 1000 individuals are tested, there are expected to be 995 non-users and 5 users. From the 995 non-users, false positives are expected. From the 5 users,
false positives are expected. From the 5 users, 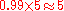 true positives are expected. Out of 15 positive results, only 5, about 33%, are genuine.
true positives are expected. Out of 15 positive results, only 5, about 33%, are genuine.
(1702–61), who studied how to compute a distribution for the probability parameter of a binomial distribution (in modern terminology). His friend Richard Price
edited and presented this work in 1763, after Bayes' death, as An Essay towards solving a Problem in the Doctrine of Chances. The French mathematician
Pierre-Simon Laplace
reproduced and extended Bayes' results in 1774, apparently quite unaware of Bayes' work. Stephen Stigler
suggested in 1983 that Bayes' theorem was discovered by Nicholas Saunderson
some time before Bayes. Edwards (1986) disputed that interpretation.
Bayes' preliminary results (Propositions 3, 4, and 5) imply the truth of the theorem that is named for him. Particularly, Proposition 5 gives a simple description of conditional probability
:
However, it does not appear that Bayes emphasized or focused on this finding. He presented his work as the solution to a problem:
Bayes gave an example of a man trying to guess the ratio of "blanks" and "prizes" at a lottery. So far the man has watched the lottery draw ten blanks and one prize. Given these data, Bayes showed in detail how to compute the probability that the ratio of blanks to prizes is between 9:1 and 11:1 (the probability is low - about 7.7%). He went on to describe that computation after the man has watched the lottery draw twenty blanks and two prizes, forty blanks and four prizes, and so on. Finally, having drawn 10,000 blanks and 1,000 prizes, the probability reaches about 97%.
Bayes' main result (Proposition 9) is the following in modern terms:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and applications, Bayes' theorem (alternatively Bayes' law or Bayes' rule) relates the conditional probabilities
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
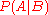 and
and  . It is commonly used in science
. It is commonly used in scienceScience
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
. The theorem is named for Thomas Bayes
Thomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
.
Under the frequentist interpretation of probability, probability measures the proportion of trials in which an event occurs. Under this interpretation, Bayes' theorem is the relationship between
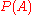 ,
, 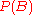 ,
, 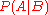 and
and  for any events
for any events  and
and  in the same event space.
in the same event space.Under the Bayesian interpretation of probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, probability, or confidence, measures the subjective confidence that something is true. Under this interpretation, Bayes' theorem links confidence before and after observing evidence.
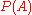 , the prior, is the initial confidence in
, the prior, is the initial confidence in  .
. 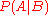 , the posterior, is the confidence having accounted for evidence
, the posterior, is the confidence having accounted for evidence  .
. 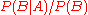 represents the degree of support
represents the degree of support  provides for
provides for  . For example, suppose somebody claims that a biased die is represented by probability model
. For example, suppose somebody claims that a biased die is represented by probability model  . The die is thrown a number of times to collect evidence,
. The die is thrown a number of times to collect evidence,  . A prior confidence of 50% may rise to a posterior of 70% if the evidence supports the model. For more detail on the application of Bayes' theorem under the Bayesian interpretation of probability, see Bayesian inference
. A prior confidence of 50% may rise to a posterior of 70% if the evidence supports the model. For more detail on the application of Bayes' theorem under the Bayesian interpretation of probability, see Bayesian inferenceBayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
.
For general events
Simple form
For events and
and  , provided that
, provided that 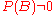 .
.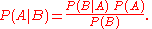
In a Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
step, the probability of evidence
 is constant for all models
is constant for all models 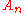 . The posterior may then be expressed as proportional
. The posterior may then be expressed as proportionalProportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the numerator:
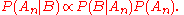
Extended form
Often, for some partitionPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the event space
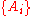 , the event space is given or conceived in terms of
, the event space is given or conceived in terms of 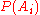 and
and  . It is then useful to eliminate
. It is then useful to eliminate  using the law of total probability
using the law of total probabilityLaw of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
:
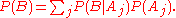

In the special case of a binary partition,
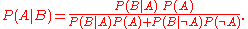
Further extensions
For more than one event, multiple hierarchical representations of a probability space exist. A simple example is shown in the figure; the simple form of Bayes' theorem connects the two representations. Extensions to Bayes' theorem may be found by relating conditional probabilities between representations for larger numbers of events. For example, for three events, two possible tree diagrams branch in the order BCA and ABC. By repeatedly applying the definition of conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
:

As previously, the law of total probability
Law of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
may be substituted for unknown marginal probabilities.
For random variables
Consider a sample space generated by two random variables
generated by two random variables  and
and  . In principle, Bayes' theorem applies to the events
. In principle, Bayes' theorem applies to the events  and
and 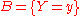 . However, terms become 0 at points where either variable has finite probability density
. However, terms become 0 at points where either variable has finite probability densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
. To remain useful, Bayes' theorem may be formulated in terms of the relevant densities (see Derivation).
Simple form
If is continuous and
is continuous and  is discrete,
is discrete,
If
 is discrete and
is discrete and  is continuous,
is continuous,
If both
 and
and  are continuous,
are continuous,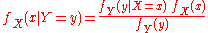
Extended form
Often, a continuous event space is given or conceived in terms of the numerator terms. It is then useful to eliminate the denominator using the law of total probabilityLaw of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
. For
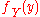 , this becomes an integral:
, this becomes an integral: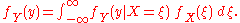
Bayes' Rule
Under the Bayesian interpretation of probabilityBayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, Bayes' rule
Bayes' rule
In probability theory and applications, Bayes' rule relates the odds of event A_1 to event A_2, before and after conditioning on event B. The relationship is expressed in terms of the Bayes factor, \Lambda. Bayes' rule is derived from and closely related to Bayes' theorem...
may be thought of as Bayes' theorem in odds form
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
.

Where
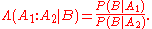
For general events
Bayes' theorem may be derived from the definition of conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
:
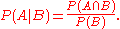
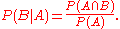
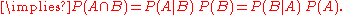

For random variables
For two continuous random variables and
and  , Bayes' theorem may be analogously derived from the definition of conditional density:
, Bayes' theorem may be analogously derived from the definition of conditional density: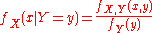
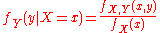
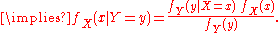
Simple example
An entomologistEntomology
Entomology is the scientific study of insects, a branch of arthropodology...
spots what might be a rare subspecies
Subspecies
Subspecies in biological classification, is either a taxonomic rank subordinate to species, ora taxonomic unit in that rank . A subspecies cannot be recognized in isolation: a species will either be recognized as having no subspecies at all or two or more, never just one...
of beetle
Beetle
Coleoptera is an order of insects commonly called beetles. The word "coleoptera" is from the Greek , koleos, "sheath"; and , pteron, "wing", thus "sheathed wing". Coleoptera contains more species than any other order, constituting almost 25% of all known life-forms...
, due to the pattern on its back. In the rare subspecies, 98% have the pattern. In the common subspecies, 5% have a similar pattern, but he cannot distinguish these from memory. The rare subspecies accounts for only 0.1% of the population. How likely is the beetle to be rare?
From the extended form of Bayes' theorem,
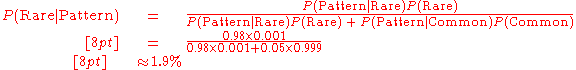
Drug testing
Suppose a drug test is 99% sensitive and 99% specific. That is, the test will produce 99% true positive and 99% true negative results. Suppose that 0.5% of people are users of the drug. If an individual tests positive, what is the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
they are a user?

Despite the apparent accuracy of the test, if an individual tests positive, it is more likely that they do not use the drug than that they do!
This surprising result arises because the number of non-users is very large compared to the number of users, such that the number of false positives (0.995%) outweighs the number of true positives (0.495%). To use concrete numbers, if 1000 individuals are tested, there are expected to be 995 non-users and 5 users. From the 995 non-users,
 false positives are expected. From the 5 users,
false positives are expected. From the 5 users, 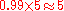 true positives are expected. Out of 15 positive results, only 5, about 33%, are genuine.
true positives are expected. Out of 15 positive results, only 5, about 33%, are genuine.Historical remarks
Bayes' theorem was named after the Reverend Thomas BayesThomas Bayes
Thomas Bayes was an English mathematician and Presbyterian minister, known for having formulated a specific case of the theorem that bears his name: Bayes' theorem...
(1702–61), who studied how to compute a distribution for the probability parameter of a binomial distribution (in modern terminology). His friend Richard Price
Richard Price
Richard Price was a British moral philosopher and preacher in the tradition of English Dissenters, and a political pamphleteer, active in radical, republican, and liberal causes such as the American Revolution. He fostered connections between a large number of people, including writers of the...
edited and presented this work in 1763, after Bayes' death, as An Essay towards solving a Problem in the Doctrine of Chances. The French mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
reproduced and extended Bayes' results in 1774, apparently quite unaware of Bayes' work. Stephen Stigler
Stephen Stigler
Stephen Mack Stigler is Ernest DeWitt Burton Distinguished Service Professor at the Department of Statistics of the University of Chicago. His research has focused on statistical theory of robust estimators and the history of statistics...
suggested in 1983 that Bayes' theorem was discovered by Nicholas Saunderson
Nicholas Saunderson
Nicholas Saunderson was an English scientist and mathematician. According to one leading historian of statistics, he may have been the earliest discoverer of Bayes theorem.-Biography:...
some time before Bayes. Edwards (1986) disputed that interpretation.
Bayes' preliminary results (Propositions 3, 4, and 5) imply the truth of the theorem that is named for him. Particularly, Proposition 5 gives a simple description of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
:
- "If there be two subsequent events, the probability of the second b/N and the probability of both together P/N, and it being first discovered that the second event has also happened, from hence I guess that the first event has also happened, the probability I am right is P/b."
However, it does not appear that Bayes emphasized or focused on this finding. He presented his work as the solution to a problem:
- "
Given the number of times in which an unknown event has happened and failed [... Find] the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named. "
Bayes gave an example of a man trying to guess the ratio of "blanks" and "prizes" at a lottery. So far the man has watched the lottery draw ten blanks and one prize. Given these data, Bayes showed in detail how to compute the probability that the ratio of blanks to prizes is between 9:1 and 11:1 (the probability is low - about 7.7%). He went on to describe that computation after the man has watched the lottery draw twenty blanks and two prizes, forty blanks and four prizes, and so on. Finally, having drawn 10,000 blanks and 1,000 prizes, the probability reaches about 97%.
Bayes' main result (Proposition 9) is the following in modern terms:
- Assume a uniform prior distribution of the binomial parameter
 . After observing
. After observing  successes and
successes and  failures,
failures,
It is unclear whether Bayes was a "Bayesian" in the modern sense. That is, whether he was interested in Bayesian inferenceInferenceInference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
, or merely in probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. Proposition 9 seems "Bayesian" in its presentation as a probability about the parameterParameterParameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
 . However, Bayes stated his question in a manner that suggests a frequentist viewpoint: he supposed that a billiard ball is thrown at random onto a billiard table, and considered further billiard balls that fall above or below the first ball with probabilities
. However, Bayes stated his question in a manner that suggests a frequentist viewpoint: he supposed that a billiard ball is thrown at random onto a billiard table, and considered further billiard balls that fall above or below the first ball with probabilities  and
and  . The algebra is of course identical no matter which view is taken.
. The algebra is of course identical no matter which view is taken.
Stephen FienbergStephen FienbergStephen Elliott Fienberg is the Maurice Falk University Professor of Statistics and Social Science in the Department of Statistics, the Machine Learning Department and Cylab at Carnegie Mellon University....
describes the evolution from "inverse probabilityInverse probabilityIn probability theory, inverse probability is an obsolete term for the probability distribution of an unobserved variable.Today, the problem of determining an unobserved variable is called inferential statistics, the method of inverse probability is called Bayesian probability, the "distribution"...
" at the time of Bayes and Laplace, a term still used by Harold JeffreysHarold JeffreysSir Harold Jeffreys, FRS was a mathematician, statistician, geophysicist, and astronomer. His seminal book Theory of Probability, which first appeared in 1939, played an important role in the revival of the Bayesian view of probability.-Biography:Jeffreys was born in Fatfield, Washington, County...
(1939), to "Bayesian" in the 1950s.
Ironically, Ronald A. Fisher introduced the "Bayesian" label in a derogatory sense.
Richard Price and the existence of God
Richard PriceRichard PriceRichard Price was a British moral philosopher and preacher in the tradition of English Dissenters, and a political pamphleteer, active in radical, republican, and liberal causes such as the American Revolution. He fostered connections between a large number of people, including writers of the...
discovered Bayes' essay and its now-famous theorem in Bayes' papers after Bayes' death. He believed that Bayes' Theorem helped prove the existence of God ("the Deity")DeityA deity is a recognized preternatural or supernatural immortal being, who may be thought of as holy, divine, or sacred, held in high regard, and respected by believers....
and wrote the following in his introduction to the essay:
- "The purpose I mean is, to shew what reason we have for believing that there are in the constitution of things fixt laws according to which things happen, and that, therefore, the frame of the world must be the effect of the wisdom and power of an intelligent cause; and thus to confirm the argument taken from final causes for the existence of the Deity. It will be easy to see that the converse problem solved in this essay is more directly applicable to this purpose; for it shews us, with distinctness and precision, in every case of any particular order or recurrency of events, what reason there is to think that such recurrency or order is derived from stable causes or regulations in nature, and not from any irregularities of chance." (Philosophical Transactions of the Royal Society of London, 1763)
In modern terms this is an instance of the teleological argumentTeleological argumentA teleological or design argument is an a posteriori argument for the existence of God based on apparent design and purpose in the universe. The argument is based on an interpretation of teleology wherein purpose and intelligent design appear to exist in nature beyond the scope of any such human...
.
Versions of the essay
- Thomas Bayes "An Essay towards solving a Problem in the Doctrine of Chances". (Bayes' essay in the original notation)
Commentaries
- G. A. BarnardGeorge Alfred BarnardGeorge Alfred Barnard was a British statistician known particularly for his work on the foundations of statistics and on quality control.-Biography:...
(1958) "Studies in the History of Probability and Statistics: IX. Thomas Bayes' Essay Towards Solving a Problem in the Doctrine of Chances", Biometrika 45:293–295. (biographical remarks) - Stephen M. Stigler (1982). "Thomas Bayes' Bayesian Inference," Journal of the Royal Statistical Society, Series A, 145:250–258. (Stigler argues for a revised interpretation of the essay; recommended)
- Isaac TodhunterIsaac TodhunterIsaac Todhunter FRS , was an English mathematician who is best known today for the books he wrote on mathematics and its history.- Life and work :...
(1865). A History of the Mathematical Theory of Probability from the time of Pascal to that of Laplace, Macmillan. Reprinted 1949, 1956 by Chelsea and 2001 by Thoemmes.
Additional material
- Laplace, Pierre-SimonPierre-Simon LaplacePierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
. (1774/1986), "Memoir on the Probability of the Causes of Events", Statistical Science 1(3):364–378. - Stephen M. Stigler (1986), "Laplace's 1774 memoir on inverse probability", Statistical Science 1(3):359–378.
- Jeff Miller, et al., Earliest Known Uses of Some of the Words of Mathematics (B). Contains origins of "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", and "Bayes Factor".
- A tutorial on probability and Bayes’ theorem devised for Oxford University psychology students
- A graphical explanation of the Bayes theorem.

