
Baum–Sweet sequence
Encyclopedia
In mathematics
the Baum–Sweet sequence is an infinite automatic sequence
of 0s and 1s defined by the rule:
for n ≥ 0.
For example, b4 = 1 because the binary representation of 4 is 100, which only contains one block of consecutive 0s of length 2; whereas b5 = 0 because the binary representation of 5 is 101, which contains a block of consecutive 0s of length 1.
Starting at n = 0, the first few terms of the Baum–Sweet sequence are:
The properties of the sequence were first studied by L.E. Baum and M.M. Sweet in 1976.
.
The value of term bn in the Baum–Sweet sequence can be found recursively as follows. If n = m·4k, where m is not divisible by 4, then
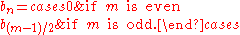
Thus b76 = b9 = b4 = b0 = 1, which can be verified by observing that the binary representation of 76, which is 1001100, contains no consecutive blocks of 0s with odd length.
The Baum–Sweet word 1101100101001001..., which is created by concatenating the terms of the Baum–Sweet sequence, is a fixed point of the morphism or string substitution rules
as follows:
From the morphism rules it can be seen that the Baum–Sweet word contains blocks of consecutive 0s of any length (bn = 0 for all 2k integers in the range 5.2k ≤ n < 6.2k), but it contains no block of three consecutive 1s.
The Baum–Sweet sequence is the sequence of coefficients of the unique solution of the cubic equation f 3 + Xf + 1 = 0 in the field F2((X −1)) of formal Laurent series
over F2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Baum–Sweet sequence is an infinite automatic sequence
Automatic sequence
An automatic sequence is an infinite sequence of terms characterized by a finite automaton. The n-th term of the sequence is a mapping of the final state of the automaton when its input is the digits of n in some fixed base k...
of 0s and 1s defined by the rule:
- bn = 1 if the binary representation of n contains no block of consecutive 0s of odd length;
- bn = 0 otherwise;
for n ≥ 0.
For example, b4 = 1 because the binary representation of 4 is 100, which only contains one block of consecutive 0s of length 2; whereas b5 = 0 because the binary representation of 5 is 101, which contains a block of consecutive 0s of length 1.
Starting at n = 0, the first few terms of the Baum–Sweet sequence are:
- 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1 ...
The properties of the sequence were first studied by L.E. Baum and M.M. Sweet in 1976.
Properties
The Baum–Sweet sequence can be generated by a three state automatonFinite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
.
The value of term bn in the Baum–Sweet sequence can be found recursively as follows. If n = m·4k, where m is not divisible by 4, then
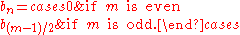
Thus b76 = b9 = b4 = b0 = 1, which can be verified by observing that the binary representation of 76, which is 1001100, contains no consecutive blocks of 0s with odd length.
The Baum–Sweet word 1101100101001001..., which is created by concatenating the terms of the Baum–Sweet sequence, is a fixed point of the morphism or string substitution rules
- 00 → 0000
- 01 → 1001
- 10 → 0100
- 11 → 1101
as follows:
- 11 → 1101 → 11011001 → 1101100101001001 → 11011001010010011001000001001001 ...
From the morphism rules it can be seen that the Baum–Sweet word contains blocks of consecutive 0s of any length (bn = 0 for all 2k integers in the range 5.2k ≤ n < 6.2k), but it contains no block of three consecutive 1s.
The Baum–Sweet sequence is the sequence of coefficients of the unique solution of the cubic equation f 3 + Xf + 1 = 0 in the field F2((X −1)) of formal Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
over F2.

