Basic affine jump diffusion
Encyclopedia
In probability theory
, a basic affine jump diffusion (basic AJD) is a stochastic process
Z of the form
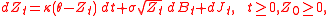
where
is a standard Brownian motion
, and
is an independent compound Poisson process
with constant jump intensity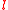
and independent exponentially distributed jumps with mean 
. For the process to be well defined, it is necessary that 
and 
. A basic AJD is a special case of an affine process and of a jump diffusion. On the other hand, the Cox–Ingersoll–Ross (CIR) process is a special case of a basic AJD.
Basic AJDs are attractive for modeling default times in credit risk
applications, since both the moment generating function
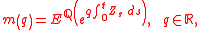
and the characteristic function
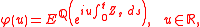
are known in closed form
.
The characteristic function allows one to calculate the density of an integrated basic AJD
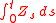
by Fourier inversion, which can be done efficiently using the FFT.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a basic affine jump diffusion (basic AJD) is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
Z of the form
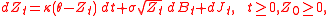
where
is a standard Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, and
is an independent compound Poisson processCompound Poisson process
A compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
with constant jump intensity
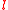and independent exponentially distributed jumps with mean . For the process to be well defined, it is necessary that and . A basic AJD is a special case of an affine process and of a jump diffusion. On the other hand, the Cox–Ingersoll–Ross (CIR) process is a special case of a basic AJD.Basic AJDs are attractive for modeling default times in credit risk
Credit risk
Credit risk is an investor's risk of loss arising from a borrower who does not make payments as promised. Such an event is called a default. Other terms for credit risk are default risk and counterparty risk....
applications, since both the moment generating function
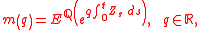
and the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
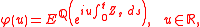
are known in closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
.
The characteristic function allows one to calculate the density of an integrated basic AJD
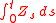
by Fourier inversion, which can be done efficiently using the FFT.