
Bailey pair
Encyclopedia
In mathematics, a Bailey pair is a pair of sequences satisfying certain relations, and a Bailey chain is a sequence of Bailey pairs. Bailey pairs were introduced by while studying
the second proof of the Rogers-Ramanujan identities
, and Bailey chains were introduced by .
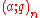 are defined as:
are defined as:
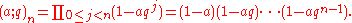
A pair of sequences (αn,βn) is called a Bailey pair if they are related by
or equivalently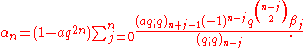
(α'n,β'n) where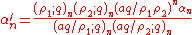
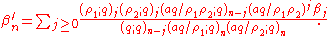
In other words, given one Bailey pair, one can construct a second using the formulas above. This process can be iterated to produce an infinite sequence of Bailey pairs, called a Bailey chain.
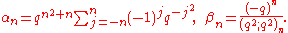
gave a list of 130 examples related to Bailey pairs.
the second proof of the Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
, and Bailey chains were introduced by .
Definition
The q-Pochhammer symbols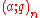 are defined as:
are defined as: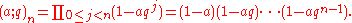
A pair of sequences (αn,βn) is called a Bailey pair if they are related by

or equivalently
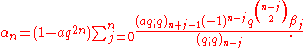
Bailey's lemma
Bailey's lemma states that if (αn,βn) is a Bailey pair, then so is(α'n,β'n) where
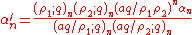
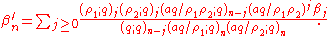
In other words, given one Bailey pair, one can construct a second using the formulas above. This process can be iterated to produce an infinite sequence of Bailey pairs, called a Bailey chain.
Examples
An example of a Bailey pair is given by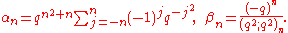
gave a list of 130 examples related to Bailey pairs.

