BHHH
Encyclopedia
BHHH is an optimization
algorithm
in econometrics
similar to Gauss–Newton algorithm. It is an acronym
of the four originators: Berndt, B. Hall, R. Hall, and Jerry Hausman.
one often needs to estimate coefficient
s through optimization
. A number of optimisation algorithms have the following general structure. Suppose that the function to be optimized is Q(β). Then the algorithms are iterative, defining a sequence of approximations, βk given by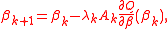
,
where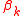
is the coefficient at step k, and 
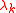is a parameter which partly determines the particular algorithm. For the BHHH algorithm λk is determined by calculations within a given iterative step, involving a line-search until a point βk+1 is found satisfying certain criteria. In addition, for the BHHH algorithm, Q has the form
and A is calculated using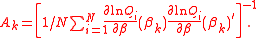
In other cases, e.g. Newton-Raphson,
can have other forms. The BHHH algorithm has the advantage that, if certain conditions apply, convergence of the iterative procedure is guaranteed.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
in econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
similar to Gauss–Newton algorithm. It is an acronym
Acronym and initialism
Acronyms and initialisms are abbreviations formed from the initial components in a phrase or a word. These components may be individual letters or parts of words . There is no universal agreement on the precise definition of the various terms , nor on written usage...
of the four originators: Berndt, B. Hall, R. Hall, and Jerry Hausman.
Usage
If a nonlinear model is fitted to the dataData
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
one often needs to estimate coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s through optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
. A number of optimisation algorithms have the following general structure. Suppose that the function to be optimized is Q(β). Then the algorithms are iterative, defining a sequence of approximations, βk given by
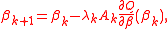,where
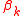is the coefficient at step k, and 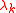is a parameter which partly determines the particular algorithm. For the BHHH algorithm λk is determined by calculations within a given iterative step, involving a line-search until a point βk+1 is found satisfying certain criteria. In addition, for the BHHH algorithm, Q has the formand A is calculated using
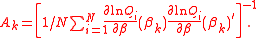
In other cases, e.g. Newton-Raphson,
can have other forms. The BHHH algorithm has the advantage that, if certain conditions apply, convergence of the iterative procedure is guaranteed.Literature
- Berndt, E., B. Hall, R. Hall, and J. Hausman, (1974), “Estimation and Inference in Nonlinear Structural Models”, Annals of Economic and Social Measurement, Vol. 3, 653–665.
- Luenberger, D. (1972), Introduction to Linear and Nonlinear Programming, Addison Wesley, Reading Massachusetts.
- Gill, P., W. Murray, and M. Wright, (1981), Practical Optimization, Harcourt Brace and Company, London
- Sokolov, S.N., and I.N. Silin (1962), “Determination of the coordinates of the minima of functionals by the linearization method”, Joint Institute for Nuclear Research preprint D-810, Dubna.