BBGKY hierarchy
Encyclopedia
In statistical physics
, the BBGKY hierarchy (Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy, sometimes called Bogoliubov hierarchy) is a set of equations describing the dynamics of a system of a large number of interacting particles. The equation for an s-particle distribution function
(probability density function) in the BBGKY hierarchy includes the (s + 1)-particle distribution function thus forming a coupled chain of equations. This formal theoretic result is named after Bogoliubov
, Born
, Green
, Kirkwood
, and Yvon.
for the probability density function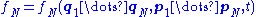
in 6N phase space
By integration over part of the variables, the Liouville equation can be transformed into a chain of equations where the first equation connects the evolution of one-particle density probability with the two-particle density probability function, second equation connects the two-particle density probability function with the three-particle probability function, and generally the s-th equation connects the s-particle density probability function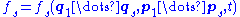
and (s+1)-particle density probability function: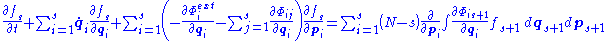
Here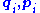
are the coordinates and momentum for ith particle, 
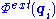is the external field potential, and 
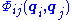is the pair potential for interaction between particles. The equation above for s-particle distribution function is obtained by integration of the Liouville equation over the variables 
.
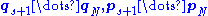s and the first order corrections to the Boltzmann equations. Other approximations, such as the assumption that the density probability function depends only on the relative distance between the particles or the assumption of the hydrodynamic regime, can also render the BBGKY chain accessible to solution.
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
, the BBGKY hierarchy (Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy, sometimes called Bogoliubov hierarchy) is a set of equations describing the dynamics of a system of a large number of interacting particles. The equation for an s-particle distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
(probability density function) in the BBGKY hierarchy includes the (s + 1)-particle distribution function thus forming a coupled chain of equations. This formal theoretic result is named after Bogoliubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
, Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
, Green
Herbert S. Green
Herbert Sydney Green was a doctoral student of the Nobel Laureate Max Born at Edinburgh, with whom he was involved in the development of the modern kinetic theory...
, Kirkwood
John Gamble Kirkwood
John "Jack" Gamble Kirkwood was a noted chemist and physicist, holding faculty positions at Cornell University, the University of Chicago, California Institute of Technology, and Yale University.-Early life and background:Kirkwood was born in Gotebo, Oklahoma, the oldest child of John Millard and...
, and Yvon.
Formulation
The evolution of an N-particle system is given by the Liouville equationLiouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
for the probability density function
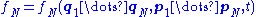in 6N phase spaceBy integration over part of the variables, the Liouville equation can be transformed into a chain of equations where the first equation connects the evolution of one-particle density probability with the two-particle density probability function, second equation connects the two-particle density probability function with the three-particle probability function, and generally the s-th equation connects the s-particle density probability function
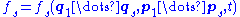and (s+1)-particle density probability function: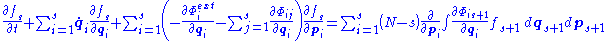Here
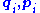are the coordinates and momentum for ith particle, 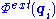is the external field potential, and 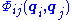is the pair potential for interaction between particles. The equation above for s-particle distribution function is obtained by integration of the Liouville equation over the variables 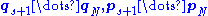.Applications
The problem of solving the BBGKY hierarchy of equations is as hard as solving the original Liouville equation, but approximations for the BBGKY hierarchy which allow to truncate the chain into a finite system of equations can readily be made. Truncation of the BBGKY chain is a common starting point for many applications of kinetic theory that can be used for derivation of classical or quantum kinetic equations. In particular, truncation at the first equation or the first two equations can be used to derive classical and quantum Boltzmann equationBoltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
s and the first order corrections to the Boltzmann equations. Other approximations, such as the assumption that the density probability function depends only on the relative distance between the particles or the assumption of the hydrodynamic regime, can also render the BBGKY chain accessible to solution.