In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

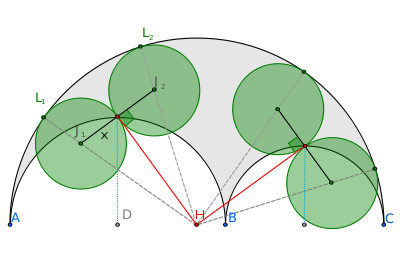
, Archimedes' quadruplets are four congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

 circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

s associated with an arbelos

Arbelos

In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...

. Introduced by Frank Power in the summer of 1998, each have the same area

Area

Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

 as Archimedes' twin circles, making them Archimedean circles.

Construction

An arbelos is formed from three collinear points A, B, and C, by the three semicircle

Semicircle

In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...

s with diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

s AB, AC, and BC. Let the two smaller circles have radii r₁ and r₂, from which it follows that the larger semicircle has radius r = r₁+r₂. Let the points D and E be the center

Centre (geometry)

In geometry, the centre of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.-Circles:...

 and midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

, respectively, of the semicircle with the radius r₁. Let H be the midpoint of line AC. Then two of the four quadruplet circles are tangent to line HE at the point E, and are also tangent to the outer semicircle. The other two quadruplet circles are formed in a symmetric way from the semicircle with radius r₂.

Proof of congruency

According to Proposition 5 of Archimedes

Archimedes

Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...

' Book of Lemmas

Book of Lemmas

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions on circles.-Translations:...

, the common radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 of Archimedes' twin circles is:


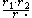
By the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

:


Then, create two circles with centers J_i perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

 to HE, tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 to the large semicircle at point L_i, tangent to point E, and with equal radii x. Using the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

:


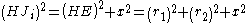
Also:


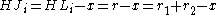
Combinding these gives:


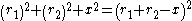
Expanding, collecting to one side, and factoring:


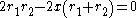
Solving for x:


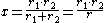
Proving that each of the Archimedes' quadruplets' areas is equal to each of Archimedes' twin circles' areas.