
Apartness relation
Encyclopedia
In constructive mathematics
, an apartness relation is a constructive form of inequality, and is often taken to be more basic than equality. It is often written as # to distinguish from the negation of equality (the denial inequality) ≠, which is weaker.
An apartness relation is a symmetric irreflexive binary relation
with the additional condition that if two elements are apart, then any other element is apart from at least one of them (this last property is often called co-transitivity or comparison).
That is, a binary relation # is an apartness relation if it satifies:
The negation
of an apartness relation is an equivalence relation
, as the above three conditions become reflexivity
, symmetry
, and transitivity
. If this equivalence relation is in fact equality, then the apartness relation is called tight. That is, # is a tight apartness relation if it additionally satisfies:
In classical
mathematics, it also follows that every apartness relation is the negation of an equivalence relation, and the only tight apartness relation on a given set is the negation of equality. So in that domain, the concept is not useful. In constructive mathematics, however, this is not the case.
The prototypical apartness relation is that of the real numbers: two real numbers are said to be apart if there exists (one can construct) a rational number
between them. In other words, real numbers x and y are apart if there exists a rational number z such that x < z < y or y < z < x. The natural apartness relation of the real numbers is then the disjunction of its natural pseudo-order
. The complex numbers, real vector spaces, and indeed any metric space
then naturally inherit the apartness relation of the real numbers, even though they do not come equipped with any natural ordering.
If there is no rational number between two real numbers, then the two real numbers are equal. Classically, then, if two real numbers are not equal, one would conclude that there exists a rational number between them. However it does not follow that one can actually construct such a number. Thus to say two real numbers are apart is a stronger statement, constructively, than to say that they are not equal, and while equality of real numbers is definable in terms of their apartness, the apartness of real numbers cannot be defined in terms of their equality. For this reason, in constructive topology especially, the apartness relation over a set is often taken as primitive, and equality is a defined relation.
A set endowed with an apartness relation is known as a constructive setoid
. A function where A and B are constructive setoids is called a morphism for #A and #B if
where A and B are constructive setoids is called a morphism for #A and #B if 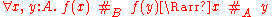 .
.
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
, an apartness relation is a constructive form of inequality, and is often taken to be more basic than equality. It is often written as # to distinguish from the negation of equality (the denial inequality) ≠, which is weaker.
An apartness relation is a symmetric irreflexive binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
with the additional condition that if two elements are apart, then any other element is apart from at least one of them (this last property is often called co-transitivity or comparison).
That is, a binary relation # is an apartness relation if it satifies:
The negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
of an apartness relation is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, as the above three conditions become reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, symmetry
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, and transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
. If this equivalence relation is in fact equality, then the apartness relation is called tight. That is, # is a tight apartness relation if it additionally satisfies:
- 4.

In classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
mathematics, it also follows that every apartness relation is the negation of an equivalence relation, and the only tight apartness relation on a given set is the negation of equality. So in that domain, the concept is not useful. In constructive mathematics, however, this is not the case.
The prototypical apartness relation is that of the real numbers: two real numbers are said to be apart if there exists (one can construct) a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
between them. In other words, real numbers x and y are apart if there exists a rational number z such that x < z < y or y < z < x. The natural apartness relation of the real numbers is then the disjunction of its natural pseudo-order
Pseudo-order
In constructive mathematics, a pseudo-order is a constructive generalisation of a linear order to the continuous case. The usual trichotomy law does not hold in the constructive continuum because of its indecomposability, so this condition is weakened....
. The complex numbers, real vector spaces, and indeed any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
then naturally inherit the apartness relation of the real numbers, even though they do not come equipped with any natural ordering.
If there is no rational number between two real numbers, then the two real numbers are equal. Classically, then, if two real numbers are not equal, one would conclude that there exists a rational number between them. However it does not follow that one can actually construct such a number. Thus to say two real numbers are apart is a stronger statement, constructively, than to say that they are not equal, and while equality of real numbers is definable in terms of their apartness, the apartness of real numbers cannot be defined in terms of their equality. For this reason, in constructive topology especially, the apartness relation over a set is often taken as primitive, and equality is a defined relation.
A set endowed with an apartness relation is known as a constructive setoid
Setoid
In mathematics, a setoid is a set equipped with an equivalence relation.Setoids are studied especially in proof theory and in type-theoretic foundations of mathematics. Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set...
. A function
 where A and B are constructive setoids is called a morphism for #A and #B if
where A and B are constructive setoids is called a morphism for #A and #B if 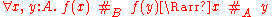 .
.




