Anonymous veto network
Encyclopedia
In cryptography, the Anonymous Veto Network (or AV-net) is a multi-party secure computation protocol to compute the boolean-OR function. It presents an efficient solution to the Dining cryptographers problem
.
with a generator 
of prime order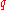 
in which the discrete logarithm problem is hard. For example, a Schnorr group can be used. For a group of 
participants, the protocol executes in two rounds.
Round 1: each participant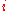
selects a random value 
and publishes the ephemeral public key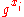 
together with a Zero-knowledge proof
for the proof of the exponent
.
After this round, each participant computes:
.
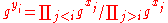Round 2: each participant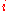
publishes 
and a Zero-knowledge proof
for the proof of the exponent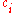
. Here, the participants chose 
if they want to send a "0" bit (no veto), or a random value if they want to send a "1" bit (veto).
After round 2, each participant computes
. If no one vetoed, each will obtain 
. On the other hand, if one or more participants vetoed, each will have 
.
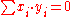. For example, if there are three participants, then 
. A similar idea - though in a non-public-key context - can be traced back to David Chaum
's original solution to the Dining cryptographers problem
.
Dining cryptographers problem
In cryptography, the dining cryptographers problem studies how to perform a secure multi-party computation of the boolean-OR function. David Chaum first proposed this problem in 1988, and used it as an illustrative example to show it was possible to send anonymous messages with unconditional sender...
.
Description
All participants agree on a group with a generator of prime order 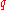in which the discrete logarithm problem is hard. For example, a Schnorr group can be used. For a group of participants, the protocol executes in two rounds.Round 1: each participant
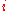selects a random value and publishes the ephemeral public key 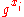together with a Zero-knowledge proofZero-knowledge proof
In cryptography, a zero-knowledge proof or zero-knowledge protocol is an interactive method for one party to prove to another that a statement is true, without revealing anything other than the veracity of the statement....
for the proof of the exponent
.After this round, each participant computes:
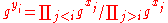.Round 2: each participant
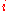publishes and a Zero-knowledge proofZero-knowledge proof
In cryptography, a zero-knowledge proof or zero-knowledge protocol is an interactive method for one party to prove to another that a statement is true, without revealing anything other than the veracity of the statement....
for the proof of the exponent
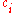. Here, the participants chose if they want to send a "0" bit (no veto), or a random value if they want to send a "1" bit (veto).After round 2, each participant computes
. If no one vetoed, each will obtain . On the other hand, if one or more participants vetoed, each will have .The protocol design
The protocol is designed by combining random public keys in such a structured way to achieve a vanishing effect. In this case,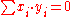. For example, if there are three participants, then . A similar idea - though in a non-public-key context - can be traced back to David ChaumDavid Chaum
David Chaum is the inventor of many cryptographic protocols, including blind signature schemes, commitment schemes, and digital cash. In 1982, Chaum founded the International Association for Cryptologic Research , which currently organizes academic conferences in cryptography research...
's original solution to the Dining cryptographers problem
Dining cryptographers problem
In cryptography, the dining cryptographers problem studies how to perform a secure multi-party computation of the boolean-OR function. David Chaum first proposed this problem in 1988, and used it as an illustrative example to show it was possible to send anonymous messages with unconditional sender...
.