Angular displacement of a body is the angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

 in radian

Radian

Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...

s (degree

Degree (angle)

A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...

s, revolutions

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

) through which a point or line has been rotated in a specified sense about a specified axis

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

.

When an object rotates about its axis, the motion cannot simply be analyzed as a particle, since in circular motion it undergoes a changing velocity and acceleration at any time (t). When dealing with the rotation of an object, it becomes simpler to consider the body itself rigid. A body is generally considered rigid when the separations between all the particles remains constant throughout the objects motion, so for example parts of its mass are not flying off. In a realistic sense, all things can be deformable, however this impact is minimal and negligible. Thus the rotation of a rigid body over a fixed axis is referred to as rotational motion.

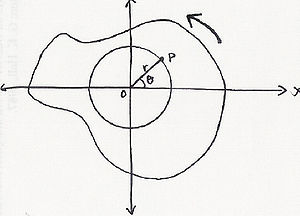
In the example illustrated to the right, a particle on object P at a fixed distance r from the origin, O, rotating counterclockwise. It becomes important to then represent the position of particle P in terms of its polar coordinates (r, θ). In this particular example, the value of θ is changing, while the value of the radius remains the same. (In rectangular coordinates (x, y) both x and y vary with time). As the particle moves along the circle, it travels an arc length

Arc (geometry)

In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...

 s, which becomes related to the angular position through the relationship:


Angular displacement is measured in radians rather than degrees. This is because it provides a very simple relationship between distance traveled around the circle and the distance r from the centre.


For example if an object rotates 360 degrees around a circle radius r the angular displacement is given by the distance traveled the circumference which is 2πr
Divided by the radius in: 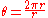which easily simplifies to . Therefore 1 revolution is radians.
When object travels from point P to point Q, as it does in the illustration to the left, over 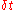the radius of the circle goes around a change in angle. 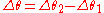which equals the Angular Displacement.

Three dimensions

In three dimensions, angular displacement is a entity with a direction and a magnitude. The direction specifies the axis of rotation, which always exists by virtue of the Euler's rotation theorem

Euler's rotation theorem

In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...

; the magnitude specifies the rotation in radians about that axis (using the right-hand rule

Right-hand rule

In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....

 to determine direction).

Despite having direction and magnitude, angular displacement is not a vector.

Matrix notation

Given that any frame in the space can be described by a rotation matrix, the displacement among them can also be described by a rotation matrix. Being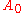 and 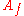two matrices, the angular displacement matrix between them can be obtained as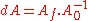

See also

• Polar moment of inertia
  Polar moment of inertia
  Polar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
  
  
• Linear elasticity
  Linear elasticity
  Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
  
  
• Infinitesimal rotations