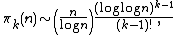Almost prime
Encyclopedia
In number theory
, a natural number
is called k-almost prime if it has exactly k prime factor
s, counted with multiplicity. More formally, a number n is k-almost prime if and only if Ω
(n) = k, where Ω(n) is the total number of primes in the prime factorization of n:
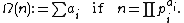
A natural number is thus prime
if and only if it is 1-almost prime, and semiprime
if and only if it is 2-almost prime. The set of k-almost primes is usually denoted by Pk. The smallest k-almost prime is 2k
. The first few k-almost primes are:
The number πk(n) of positive integers less than or equal to n with at most k prime divisors (not necessarily distinct) is asymptotic
to
a result of Landau
. See also the Hardy–Ramanujan theorem
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
is called k-almost prime if it has exactly k prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s, counted with multiplicity. More formally, a number n is k-almost prime if and only if Ω
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n) = k, where Ω(n) is the total number of primes in the prime factorization of n:
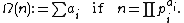
A natural number is thus prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
if and only if it is 1-almost prime, and semiprime
Semiprime
In mathematics, a semiprime is a natural number that is the product of two prime numbers. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... ....
if and only if it is 2-almost prime. The set of k-almost primes is usually denoted by Pk. The smallest k-almost prime is 2k
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
. The first few k-almost primes are:
-
k k-almost primes OEIS sequence 1 2, 3, 5, 7, 11, 13, 17, 19, … 2 4, 6, 9, 10, 14, 15, 21, 22, … 3 8, 12, 18, 20, 27, 28, 30, … 4 16, 24, 36, 40, 54, 56, 60, … 5 32, 48, 72, 80, 108, 112, … 6 64, 96, 144, 160, 216, 224, … 7 128, 192, 288, 320, 432, 448, … 8 256, 384, 576, 640, 864, 896, … 9 512, 768, 1152, 1280, 1728, … 10 1024, 1536, 2304, 2560, … 11 2048, 3072, 4608, 5120, … 12 4096, 6144, 9216, 10240, … 13 8192, 12288, 18432, 20480, … 14 16384, 24576, 36864, 40960, … 15 32768, 49152, 73728, 81920, … 16 65536, 98304, 147456, … 17 131072, 196608, 294912, … 18 262144, 393216, 589824, … 19 524288, 786432, 1179648, … 20 1048576, 1572864, 2359296, …
The number πk(n) of positive integers less than or equal to n with at most k prime divisors (not necessarily distinct) is asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
to
a result of Landau
Edmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
. See also the Hardy–Ramanujan theorem
Hardy–Ramanujan theorem
In mathematics, the Hardy–Ramanujan theorem, proved by , states that the normal order of the number ω of distinct prime factors of a number n is log...
.