
Hardy–Ramanujan theorem
Encyclopedia
In mathematics, the Hardy–Ramanujan theorem, proved by , states that the normal order
of the number ω(n) of distinct prime factor
s of a number n is log(log(n)). Roughly speaking, this means that most numbers have about this number of distinct prime factors.
A more precise version states that for any real-valued function ψ(n) that tends to infinity as n tends to infinity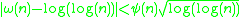
or more traditionally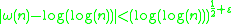
for almost all
(all but an infinitesimal proportion of) integers. That is, let g(x) be the number of positive integers n less than x for which the above inequality fails: then g(x)/x converges to zero as x goes to infinity.)
A simple proof to the result was given by Pál Turán
.
The same results are true of Ω(n), the number of prime factors of n counted with multiplicity
.
This theorem is generalized by the Erdős–Kac theorem
, which shows in fact that distinct prime factors are essentially normally distributed.
Normal order of an arithmetic function
In number theory, the normal order of an arithmetic function is some simpler or better-understood function which "usually" takes the same or closely approximate values.Let ƒ be a function on the natural numbers...
of the number ω(n) of distinct prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s of a number n is log(log(n)). Roughly speaking, this means that most numbers have about this number of distinct prime factors.
A more precise version states that for any real-valued function ψ(n) that tends to infinity as n tends to infinity
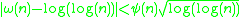
or more traditionally
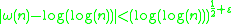
for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
(all but an infinitesimal proportion of) integers. That is, let g(x) be the number of positive integers n less than x for which the above inequality fails: then g(x)/x converges to zero as x goes to infinity.)
A simple proof to the result was given by Pál Turán
Pál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
.
The same results are true of Ω(n), the number of prime factors of n counted with multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
.
This theorem is generalized by the Erdős–Kac theorem
Erdos–Kac theorem
In number theory, the Erdős–Kac theorem, named after Paul Erdős and Mark Kac, and also known as the fundamental theorem of probabilistic number theory, states that if ω is the number of distinct prime factors of n, then, loosely speaking, the probability distribution ofis the standard normal...
, which shows in fact that distinct prime factors are essentially normally distributed.

