
Algebraically compact group
Encyclopedia
In mathematics
, in the realm of abelian
group theory
, a group
is said to be algebraically compact if it is a direct summand of every abelian group containing it as a pure subgroup
.
Equivalent characterizations of algebraic compactness:
Relations with other properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the realm of abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is said to be algebraically compact if it is a direct summand of every abelian group containing it as a pure subgroup
Pure subgroup
In mathematics, especially in the area of algebra studying the theory of abelian groups, a pure subgroup is a generalization of direct summand. It has found many uses in abelian group theory and related areas.-Definition:...
.
Equivalent characterizations of algebraic compactness:
- The group is complete in the
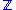 adic topology.
adic topology. - The group is pure injective, that is, injective with respect to exact sequences where the embedding is as a pure subgroup.
Relations with other properties:
- A torsion-free group is cotorsionCotorsion groupIn mathematics, in the realm of abelian group theory, an abelian group is said to be cotorsion if every extension of it by a torsion-free group splits. If the group is C, this is equivalent to asserting that Ext = 0 for all torsion-free groups G...
if and only if it is algebraically compact. - Every injective group is algebraically compact.
- Ulm factors of cotorsion groups are algebraically compact.

