
Actuarial reserves
Encyclopedia
An actuarial reserve is a liability equal to the net present value
of the future expected cash flows of a contingent event. In the insurance context an actuarial reserve is the present value of the future cash flows of an insurance policy and the total liability of the insurer is the sum of the actuarial reserves for every individual policy. Regulated insurers are required to keep offsetting assets to pay off this future liability.
is the starting point in the determination of any type of actuarial reserve calculation. Define to be the future curtate lifetime random variable of a person aged x. Then, for a death benefit of one dollar and premium
to be the future curtate lifetime random variable of a person aged x. Then, for a death benefit of one dollar and premium 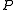 , the loss random variable,
, the loss random variable, 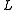 , can be written in actuarial notation
, can be written in actuarial notation
as a function of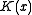

From this we can see that the present value of the loss to the insurance company now if the person dies in t years, is equal to the present value of the death benefit minus the present value of the premiums.
The loss random variable described above only defines the loss at issue. For K(x)>t, the loss random variable at time t can be defined as:
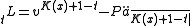
reporting purposes. The valuation premium in an NLP reserve is a premium such that the value of the reserve at time zero is equal to zero. The net level premium reserve is found by taking the expected value of the loss random variable defined above. They can be formulated prospectively or retrospectively. The amount of prospective reserves at a point in time is derived by subtracting the actuarial present value
of future valuation premiums from the actuarial present value of the future insurance benefits. Retrospective reserving subtracts accumulated value of benefits from accumulated value of valuation premiums as of a point in time. The two methods yield identical results (assuming bases are the same for both prospective and retrospective calculations).
As an example, consider a whole life insurance policy of one dollar issues on (x) with yearly premiums paid at the start of the year and death benefit paid at the end of the year. In actuarial notation, a benefit reserve is denoted as V. Our objective is to find the value of the net level premium reserve at time t. First we define the loss random variable at time zero for this policy. Hence
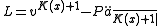
Then, taking expected values we have: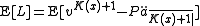
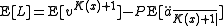
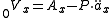
Setting the reserve equal to zero and solving for P yields:
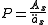
For a whole life policy as defined above the premium is denoted as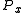 in actuarial notation.
in actuarial notation.
The NLP reserve at time t is the expected value of the loss random variable at time t given K(x)>t

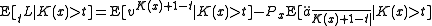
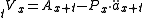 Where
Where 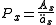
For example, if we expect to pay $300,000 in Year 1, $200,000 in year 2 and $150,000 in Year 3, and we are able to invest reserves to earn 8%p.a., the respective contributions to Actuarial Reserves are:
If we sum the discounted expected claims over all years in which a claim could be experienced, we have completed the computation of Actuarial Reserves. In the above example, if there were no expected future claims after year 3, our computation would give Actuarial Reserves of $568,320.38.
Net present value
In finance, the net present value or net present worth of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values of the individual cash flows of the same entity...
of the future expected cash flows of a contingent event. In the insurance context an actuarial reserve is the present value of the future cash flows of an insurance policy and the total liability of the insurer is the sum of the actuarial reserves for every individual policy. Regulated insurers are required to keep offsetting assets to pay off this future liability.
The Loss Random Variable
The loss random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is the starting point in the determination of any type of actuarial reserve calculation. Define
 to be the future curtate lifetime random variable of a person aged x. Then, for a death benefit of one dollar and premium
to be the future curtate lifetime random variable of a person aged x. Then, for a death benefit of one dollar and premium 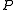 , the loss random variable,
, the loss random variable, 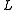 , can be written in actuarial notation
, can be written in actuarial notationActuarial notation
Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.Traditional notation uses a halo system where symbols are placed as superscript or subscript before or after the main letter...
as a function of
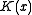

From this we can see that the present value of the loss to the insurance company now if the person dies in t years, is equal to the present value of the death benefit minus the present value of the premiums.
The loss random variable described above only defines the loss at issue. For K(x)>t, the loss random variable at time t can be defined as:
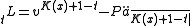
Net Level Premium Reserves
Net level premium reserves, also called benefit reserves, only involve two cash flows and are used for some USGAAPGenerally Accepted Accounting Principles (USA)
In the U.S., Generally Accepted Accounting Principles are accounting rules used to prepare, present, and report financial statements for a wide variety of entities, including publicly traded and privately held companies, non-profit organizations, and governments. The term is usually confined to the...
reporting purposes. The valuation premium in an NLP reserve is a premium such that the value of the reserve at time zero is equal to zero. The net level premium reserve is found by taking the expected value of the loss random variable defined above. They can be formulated prospectively or retrospectively. The amount of prospective reserves at a point in time is derived by subtracting the actuarial present value
Actuarial present value
In actuarial science, the actuarial present value of a payment or series of payments which are random variables is the expected value of the present value of the payments, or equivalently, the present value of their expected values....
of future valuation premiums from the actuarial present value of the future insurance benefits. Retrospective reserving subtracts accumulated value of benefits from accumulated value of valuation premiums as of a point in time. The two methods yield identical results (assuming bases are the same for both prospective and retrospective calculations).
As an example, consider a whole life insurance policy of one dollar issues on (x) with yearly premiums paid at the start of the year and death benefit paid at the end of the year. In actuarial notation, a benefit reserve is denoted as V. Our objective is to find the value of the net level premium reserve at time t. First we define the loss random variable at time zero for this policy. Hence
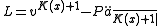
Then, taking expected values we have:
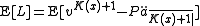
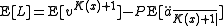
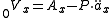
Setting the reserve equal to zero and solving for P yields:
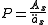
For a whole life policy as defined above the premium is denoted as
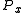 in actuarial notation.
in actuarial notation.The NLP reserve at time t is the expected value of the loss random variable at time t given K(x)>t

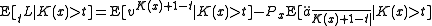
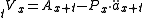 Where
Where 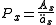
Computation of actuarial reserves
The calculation process often involves a number of assumptions, particularly in relation to future claims experience, and investment earnings potential. Generally, the computation involves calculating the expected claims for each future time period. These expected future cash outflows are then discounted to reflect interest to the date of the expected cash flow.For example, if we expect to pay $300,000 in Year 1, $200,000 in year 2 and $150,000 in Year 3, and we are able to invest reserves to earn 8%p.a., the respective contributions to Actuarial Reserves are:
- Year 1: $300,000 x (1.08)−1 = $277,777.78
- Year 2: $200,000 x (1.08)−2 = $171,467.76
- Year 3: $150,000 x (1.08)−3 = $119,074.84.
If we sum the discounted expected claims over all years in which a claim could be experienced, we have completed the computation of Actuarial Reserves. In the above example, if there were no expected future claims after year 3, our computation would give Actuarial Reserves of $568,320.38.
See also
- Actuarial scienceActuarial scienceActuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
- ActuaryActuaryAn actuary is a business professional who deals with the financial impact of risk and uncertainty. Actuaries provide expert assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms ....
- Force of mortalityForce of mortalityIn actuarial science, force of mortality represents the instantaneous rate of mortality at a certain age measured on an annualized basis. It is identical in concept to failure rate, also called hazard function, in reliability theory....
- Life insuranceLife insuranceLife insurance is a contract between an insurance policy holder and an insurer, where the insurer promises to pay a designated beneficiary a sum of money upon the death of the insured person. Depending on the contract, other events such as terminal illness or critical illness may also trigger...
- Life tableLife tableIn actuarial science, a life table is a table which shows, for each age, what the probability is that a person of that age will die before his or her next birthday...
- Statutory reserveStatutory reserveIn the business of insurance, statutory reserves are those liabilities an insurance company is legally required to maintain on its balance sheet with respect to the unmatured obligations of the company.-Life insurance:...

