
Activation function
Encyclopedia
In computational networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the behavior of the linear perceptron in neural networks
. However, it is the nonlinear activation function that allows such networks to compute nontrivial problems using only a small number of nodes.
firing in the cell. In its simplest form, this function is binary
--that is, either the neuron
is firing or not. The function looks like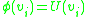 , where
, where 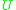 is the Heaviside step function
is the Heaviside step function
. In this case a large number of neurons must be used in computation beyond linear separation of categories.
A line of positive slope
may also be used to reflect the increase in firing rate that occurs as input current increases. The function would then be of the form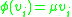 , where
, where 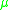 is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizable
is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizable
.
All problems mentioned above can be handled by using a normalizable sigmoid
activation function. One realistic model stays at zero until input current is received, at which point the firing frequency increases quickly at first, but gradually approaches an asymptote
at 100% firing rate. Mathematically, this looks like , where the hyperbolic tangent function can also be any sigmoid. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement in order to calculate backpropagation
, where the hyperbolic tangent function can also be any sigmoid. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement in order to calculate backpropagation
.
The final model, then, that is used in multilayer perceptrons
is a sigmoidal activation function in the form of a hyperbolic tangent. Two forms of this function are commonly used: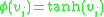 whose range is normalized from -1 to 1, and
whose range is normalized from -1 to 1, and  is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types of computational problems.
is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types of computational problems.
(RBFs) are used in RBF networks
, which are extremely efficient as universal function approximators. These activation functions can take any form, but they are usually found as one of three functions:
where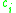 is the vector representing the function center and
is the vector representing the function center and  and
and  are parameters affecting the spread of the radius.
are parameters affecting the spread of the radius.
Support vector machines (SVMs) can effectively utilize a class of activation functions that includes both sigmoids and RBFs. In this case, the input is transformed to reflect a decision boundary hyperplane based on a few training inputs called support vectors . The activation function for the hidden layer of these machines is referred to as the inner product kernel,
. The activation function for the hidden layer of these machines is referred to as the inner product kernel, 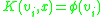 . The support vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as
. The support vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as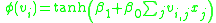 ,
,
where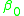 and
and 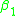 must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where
must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where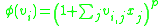 .
.
activation function having types:-
1.idetity function.
2.Binary step function.
3.bipolar step function.
4.Sigmoidal function.
a.Binary sigmoidal function.
b.bipolar sigmoidal function.
5.Ramp function.
Neural Networks
Neural Networks is the official journal of the three oldest societies dedicated to research in neural networks: International Neural Network Society, European Neural Network Society and Japanese Neural Network Society, published by Elsevier...
. However, it is the nonlinear activation function that allows such networks to compute nontrivial problems using only a small number of nodes.
Functions
In biologically-inspired neural networks, the activation function is usually an abstraction representing the rate of action potentialAction potential
In physiology, an action potential is a short-lasting event in which the electrical membrane potential of a cell rapidly rises and falls, following a consistent trajectory. Action potentials occur in several types of animal cells, called excitable cells, which include neurons, muscle cells, and...
firing in the cell. In its simplest form, this function is binary
Binary function
In mathematics, a binary function, or function of two variables, is a function which takes two inputs.Precisely stated, a function f is binary if there exists sets X, Y, Z such that\,f \colon X \times Y \rightarrow Z...
--that is, either the neuron
Neuron
A neuron is an electrically excitable cell that processes and transmits information by electrical and chemical signaling. Chemical signaling occurs via synapses, specialized connections with other cells. Neurons connect to each other to form networks. Neurons are the core components of the nervous...
is firing or not. The function looks like
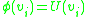 , where
, where 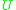 is the Heaviside step function
is the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. In this case a large number of neurons must be used in computation beyond linear separation of categories.
A line of positive slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
may also be used to reflect the increase in firing rate that occurs as input current increases. The function would then be of the form
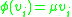 , where
, where 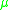 is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizable
is the slope. This activation function is linear, and therefore has the same problems as the binary function. In addition, networks constructed using this model have unstable convergence because neuron inputs along favored paths tend to increase without bound, as this function is not normalizableNormalization
Normalization may refer to:- Mathematics and statistics:* Normalization property , term in mathematical logic and theoretical computer science* Noether normalization lemma, result of commutative algebra...
.
All problems mentioned above can be handled by using a normalizable sigmoid
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
activation function. One realistic model stays at zero until input current is received, at which point the firing frequency increases quickly at first, but gradually approaches an asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
at 100% firing rate. Mathematically, this looks like
 , where the hyperbolic tangent function can also be any sigmoid. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement in order to calculate backpropagation
, where the hyperbolic tangent function can also be any sigmoid. This behavior is realistically reflected in the neuron, as neurons cannot physically fire faster than a certain rate. This model runs into problems, however, in computational networks as it is not differentiable, a requirement in order to calculate backpropagationBackpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
.
The final model, then, that is used in multilayer perceptrons
Multilayer perceptron
A multilayer perceptron is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a...
is a sigmoidal activation function in the form of a hyperbolic tangent. Two forms of this function are commonly used:
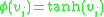 whose range is normalized from -1 to 1, and
whose range is normalized from -1 to 1, and  is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types of computational problems.
is vertically translated to normalize from 0 to 1. The latter model is often considered more biologically realistic, but it runs into theoretical and experimental difficulties with certain types of computational problems.Alternative structures
A special class of activation functions known as radial basis functionsRadial basis function
A radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
(RBFs) are used in RBF networks
Radial basis function network
A radial basis function network is an artificial neural network that uses radial basis functions as activation functions. It is a linear combination of radial basis functions...
, which are extremely efficient as universal function approximators. These activation functions can take any form, but they are usually found as one of three functions:
- Gaussian:
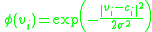
- Multiquadratics:
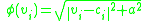
- Inverse multiquadratics:
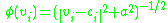
where
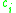 is the vector representing the function center and
is the vector representing the function center and  and
and  are parameters affecting the spread of the radius.
are parameters affecting the spread of the radius.Support vector machines (SVMs) can effectively utilize a class of activation functions that includes both sigmoids and RBFs. In this case, the input is transformed to reflect a decision boundary hyperplane based on a few training inputs called support vectors
 . The activation function for the hidden layer of these machines is referred to as the inner product kernel,
. The activation function for the hidden layer of these machines is referred to as the inner product kernel, 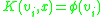 . The support vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as
. The support vectors are represented as the centers in RBFs with the kernel equal to the activation function, but they take a unique form in the perceptron as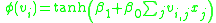 ,
,where
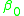 and
and 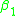 must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where
must satisfy certain conditions for convergence. These machines can also accept arbitrary-order polynomial activation functions where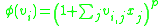 .
. activation function having types:-
1.idetity function.
2.Binary step function.
3.bipolar step function.
4.Sigmoidal function.
a.Binary sigmoidal function.
b.bipolar sigmoidal function.
5.Ramp function.

