Abbe sine condition
Encyclopedia
The Abbe sine condition is a condition that must be fulfilled by a lens
or other optical system in order for it to produce sharp images of off-axis as well as on-axis objects. It was formulated by Ernst Abbe in the context of microscope
s.
The mathematical condition is as follows:
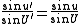
where the variables u, U are the angles (relative to the optic axis) of any two rays as they leave the object, and u’, U’ are the angles of the same rays where they reach the image plane (say, the film plane of a camera). For example, (u,u’) might represent a paraxial ray (i.e. a ray nearly parallel with the optic axis), and (U,U’) might represent a marginal ray (i.e. a ray with the largest angle admitted by the system aperture); the condition is general, however, and does not only apply to those rays.
Put in words, the sine
of the output angle should be proportional to the sine of the input angle.
, we may easily explain the significance of the Abbe sine condition. Say an object in the object plane of an optical system has a transmittance function of the form, T(xo,yo). We may express this transmittance function in terms of its Fourier transform
as
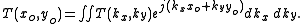
Now, assume for simplicity that the system has no image distortion, so that the image plane coordinates are linearly related to the object plane coordinates via the relation
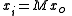
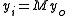
where M is the system magnification
. Let's now re-write the object plane transmittance above in a slightly modified form:
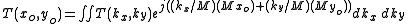
where we have simply multiplied and divided the various terms in the exponent by M, the system magnification. Now, we may substitute the equations above for image plane coordinates in terms of object plane coordinates, to obtain,
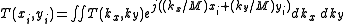
At this point we can propose another coordinate transformation (i.e., the Abbe sine condition) relating the object plane wavenumber
spectrum to the image plane wavenumber spectrum as
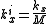
to obtain our final equation for the image plane field in terms of image plane coordinates and image plane wavenumbers as:
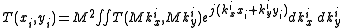
From Fourier optics
, we know that the wavenumbers can be expressed in terms of the spherical coordinate system
as
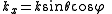
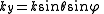
If we consider a spectral component for which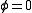
, then the coordinate transformation between object and image plane wavenumbers takes the form
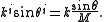
This is another way of writing the Abbe sine condition, which simply reflects Heisenberg's uncertainty principle
for Fourier transform pairs, namely that as the spatial extent of any function is expanded (by the magnification factor, M), the spectral extent contracts by the same factor, M, so that the space-bandwidth product remains constant.
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
or other optical system in order for it to produce sharp images of off-axis as well as on-axis objects. It was formulated by Ernst Abbe in the context of microscope
Microscope
A microscope is an instrument used to see objects that are too small for the naked eye. The science of investigating small objects using such an instrument is called microscopy...
s.
The mathematical condition is as follows:
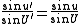
where the variables u, U are the angles (relative to the optic axis) of any two rays as they leave the object, and u’, U’ are the angles of the same rays where they reach the image plane (say, the film plane of a camera). For example, (u,u’) might represent a paraxial ray (i.e. a ray nearly parallel with the optic axis), and (U,U’) might represent a marginal ray (i.e. a ray with the largest angle admitted by the system aperture); the condition is general, however, and does not only apply to those rays.
Put in words, the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of the output angle should be proportional to the sine of the input angle.
Magnification and the Abbe sine condition
Using the framework of Fourier opticsFourier optics
Fourier optics is the study of classical optics using Fourier transforms and can be seen as the dual of the Huygens-Fresnel principle. In the latter case, the wave is regarded as a superposition of expanding spherical waves which radiate outward from actual current sources via a Green's function...
, we may easily explain the significance of the Abbe sine condition. Say an object in the object plane of an optical system has a transmittance function of the form, T(xo,yo). We may express this transmittance function in terms of its Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
as
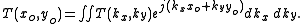
Now, assume for simplicity that the system has no image distortion, so that the image plane coordinates are linearly related to the object plane coordinates via the relation
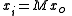
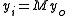
where M is the system magnification
Magnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
. Let's now re-write the object plane transmittance above in a slightly modified form:
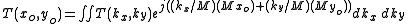
where we have simply multiplied and divided the various terms in the exponent by M, the system magnification. Now, we may substitute the equations above for image plane coordinates in terms of object plane coordinates, to obtain,
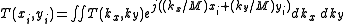
At this point we can propose another coordinate transformation (i.e., the Abbe sine condition) relating the object plane wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
spectrum to the image plane wavenumber spectrum as
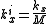
to obtain our final equation for the image plane field in terms of image plane coordinates and image plane wavenumbers as:
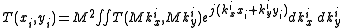
From Fourier optics
Fourier optics
Fourier optics is the study of classical optics using Fourier transforms and can be seen as the dual of the Huygens-Fresnel principle. In the latter case, the wave is regarded as a superposition of expanding spherical waves which radiate outward from actual current sources via a Green's function...
, we know that the wavenumbers can be expressed in terms of the spherical coordinate system
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
as
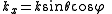
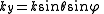
If we consider a spectral component for which
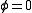, then the coordinate transformation between object and image plane wavenumbers takes the form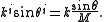This is another way of writing the Abbe sine condition, which simply reflects Heisenberg's uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
for Fourier transform pairs, namely that as the spatial extent of any function is expanded (by the magnification factor, M), the spectral extent contracts by the same factor, M, so that the space-bandwidth product remains constant.