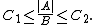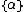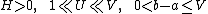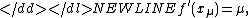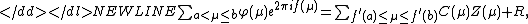History of the problem

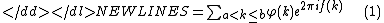
are under study.

Here and 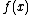are real valued functions of a real
argument, and
Such sums appear, for example, in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

 in the analysis of the
Riemann zeta function, in the solution of problems connected with
integer points in the domains on plane and in space, in the study of the
Fourier series

Fourier series

In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

, and in the solution of such differential equations as the wave equation

Wave equation

The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...

, the potential equation, the heat conductivity

Heat equation

The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...

 equation.

The problem of approximation of the series (1) by a suitable function was studied already by Euler

Leonhard Euler

Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...

 and
Poisson

Siméon Denis Poisson

Siméon Denis Poisson , was a French mathematician, geometer, and physicist. He however, was the final leading opponent of the wave theory of light as a member of the elite l'Académie française, but was proven wrong by Augustin-Jean Fresnel.-Biography:...

.

We shall define
the length of the sum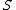
to be the number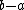
(for the integers and this is the number of the summands in ).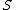

Under certain conditions on and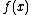
the sum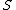 can be
substituted with good accuracy by another sum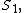

where the length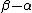 is far less than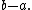

First relations of the form

where 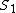are the sums (1) and (2) respectively, 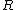is
a remainder term, with concrete functions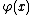 and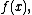
were obtained by G. H. Hardy

G. H. Hardy

Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....

 and J. E. Littlewood ,,
when they
deduced approximate functional equation for the Riemann zeta function
$\zeta(s)$ and by I. M. Vinogradov , in the study of
the amounts of integer points in the domains on plane.
In general form the theorem
was proved by J. Van der Corput

Johannes van der Corput

Johannes Gualtherus van der Corput was a Dutch mathematician, working in the field of analytic number theory....

 , (on the recent
results connected with the Van der Corput theorem one can read at
).

In every one of the above-mentioned works,
some restrictions on the functions
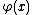and 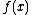were imposed. With
convenient (for applications) restrictions on
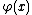and the theorem was proved by A. A. Karatsuba

Anatolii Alexeevitch Karatsuba

Anatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...

in (see also ,).

Certain notations

[1]. For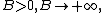
or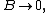 the record


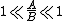
means that there are the constants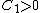
and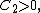
such that

[2]. For a real number the record
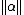means that

where

is the fractional part of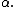

ATS theorem

Let the real functions ƒ(x) and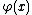 satisfy on the segment [a, b] the following conditions:

1)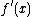 and 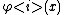are continuous;

2) there exist numbers
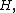
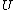and such that

and

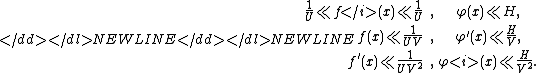
Then, if we define the numbers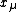 from the equation

we have

where

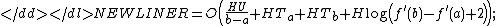
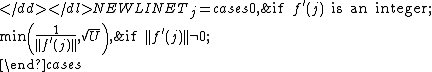
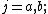
The most simple variant of the formulated theorem is the statement, which is called in the literature the Van der Corput lemma.

Van der Corput lemma

Let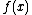 be a real differentiable function in the interval
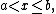moreover, inside of this interval, its derivative
is a monotonic and a sign-preserving function, and for the constant 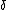such that 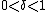satisfies the inequality
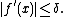Then

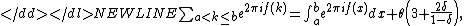
where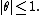

Remark

If the parameters and are integers, then it is possible to substitute the last relation by the following ones:

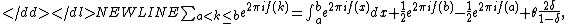
where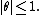

On the applications of ATS to the problems of physics see ,; see also ,.

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.