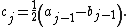AGM method
Encyclopedia
In mathematics, the AGM method (for arithmetic-geometric mean) makes it possible to construct fast algorithm
s for calculation of exponential
and trigonometric functions, and some mathematical constant
s and in particular, to quickly compute .
.
Gauss
noticed that the sequences
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s for calculation of exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and trigonometric functions, and some mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s and in particular, to quickly compute
 .
.Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
noticed that the sequences
-
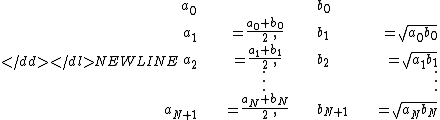
have for
the same limit:
-
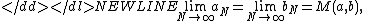
the arithmetic-geometric mean.
It is possible to use this fact to construct fast algorithms for calculation of elementary transcendental functionTranscendental functionA transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s and some classical constants and in particular, to quickly calculate the constant .
.
For example, according to the Gauss–Salamin formula:
-

where
At the same time, if we take
-
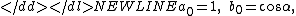
then
-
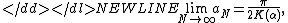
where K(α) is a complete elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
-
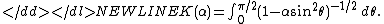
Using this property of the AGM and also the ascending transformations of Landen, Richard BrentRichard Brent (scientist)Richard Peirce Brent is an Australian mathematician and computer scientist, born in 1946. He holds the position of Distinguished Professor of Mathematics and Computer Science with a joint appointment in the Mathematical Sciences Institute and the College of Engineering and Computer Science at...
suggested the first AGM algorithms for fast evaluation of elementary transcendental functions (ex, cos x, sin x). Later many authors have been going on to study and use the AGM algorithms, see, for example, the book "Pi and the AGM" by JonathanJonathan BorweinJonathan Michael Borwein is a Scottish mathematician who holds an appointment as Laureate Professor of mathematics at the University of Newcastle, Australia. Noted for his prolific and creative work throughout the international mathematical community, he is a close associate of David H...
and Peter BorweinPeter BorweinPeter Benjamin Borwein is a Canadian mathematicianand a professor at Simon Fraser University. He is known as a co-discoverer of the Bailey-Borwein-Plouffe algorithm for computing π.-First interest in mathematics:...
.
-
-
-
-
-