
53 equal temperament
Encyclopedia
In music, 53 equal temperament, called 53-TET, 53-EDO, or 53-ET, is the tempered scale derived by dividing the octave into 53 equal steps (equal frequency ratios). Each step represents a frequency ratio of 21/53, or 22.6415 cents
, an interval sometimes called the Holdrian comma.
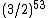 ) is very nearly equal to 31 octaves (
) is very nearly equal to 31 octaves (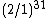 ). He calculated this difference with six-digit accuracy to be
). He calculated this difference with six-digit accuracy to be 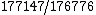 . Later the same observation was made by the mathematician and music theorist Nicholas Mercator
. Later the same observation was made by the mathematician and music theorist Nicholas Mercator
(c. 1620–1687), who calculated this value precisely as , which is known as Mercator's comma. Mercator's comma is of such small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1/53 of that comma (≈ 0.0682 cent ≈ 1/315 syntonic comma
, which is known as Mercator's comma. Mercator's comma is of such small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1/53 of that comma (≈ 0.0682 cent ≈ 1/315 syntonic comma
). Thus, 53 equal temperament is for all practical purposes equivalent to an extended Pythagorean tuning
.
After Mercator, William Holder
published a treatise in 1694 which pointed out that 53 equal temperament also very closely approximates the just major third (to within 1.4 cents), and consequently 53 equal temperament accommodates the intervals of 5-limit
just intonation very well. This property of 53-TET may have been known earlier; Isaac Newton
's unpublished manuscripts suggest that he had been aware of it as early as 1664–65.
perfect fifth
, this scale can practically be considered a form of Pythagorean tuning
that has been extended to 53 tones. As such the intervals available can have the same properties as any Pythagorean tuning, such as fifths that are (practically) pure, major thirds that are wide from just (about 81/64 opposed to the purer 5/4), and minor thirds that are conversely narrow (32/27 compared to 6/5).
However, unlike most Pythagorean forms of tuning, 53-TET contains additional intervals that are very close to just intonation. For instance, the interval of 17 steps is also a major third, but only 1.4 cents narrower than the very pure just interval 5/4. 53-TET is very good as an approximation to any interval in 5-limit just intonation.
, and 15625/15552, known as the kleisma
. These are both 5-limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53-et tempers out both characterizes it completely as a 5-limit temperament: it is the only regular temperament
tempering out both of these intervals, or comma
s, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka
. Because it tempers these out, 53-et can be used for both schismatic temperament
, tempering out the schisma, and Hanson temperament (also called kleismic), tempering out the kleisma.
The interval of 7/4 is 4.8 cents sharp in 53-et, and using it for 7-limit harmony means that the septimal kleisma
, the interval 225/224, is also tempered out.
and 31-ET
where there is little ambiguity. By not being meantone, it adds some problems that require more attention. Specifically, the major third is different from a ditone, two tones, each of which is two fifths minus an octave. Likewise, the minor third is different from a semiditone.
The fact that the syntonic comma
is not tempered out means that things (notes, intervals) need to be defined more precisely.
tuning. Instead, the major triads are chords like C-Fb-G, where the major third is a diminished fourth; this is the defining characteristic of schismatic temperament
. Likewise, the minor triads are chords like C-D#-G. In 53-et the dominant seventh chord
would be spelled C-Fb-G-Bb, but the otonal tetrad is C-Fb-G-Cbb, and C-Fb-G-A# is still another seventh chord. The utonal tetrad, the inversion of the otonal tetrad, is spelled C-D#-G-Gx.
Further septimal chords are the diminished triad, having the two forms C-D#-Gb and C-Fbb-Gb, the subminor triad, C-Fbb-G, the supermajor triad C-Dx-G, and corresponding tetrads C-Fbb-G-Bbb and C-Dx-G-A#. Since 53-et tempers out the septimal kleisma
, the septimal kleisma augmented triad C-Fb-Bbb in its various inversions is also a chord of the system. So is the orwell tetrad, C-Fb-Dxx-Gx in its various inversions.
music. Such instruments were devised by RHM Bosanquet
and the American tuner James Paul White. Subsequently the temperament has seen occasional use by composers in the west, and has been used in Turkish music
as well; the Turkish composer Erol Sayan has employed it, following theoretical use of it by Turkish music theorist Kemal Ilerici. Arabic music, which for the most part bases its theory on quartertones, has also made some use of it; the Syrian violinist and music theorist Twfiq Al-Sabagh proposed that instead of an equal division of the octave into 24 parts a 24-note scale in 53-et should be used as the master
scale for Arabic music.
Croatian composer Josip Štolcer-Slavenski
wrote one piece, which has never been published, which uses Bosanquet's Enharmonium
during its first movement, entitled Music for Natur-ton-system.
Cent (music)
The cent is a logarithmic unit of measure used for musical intervals. Twelve-tone equal temperament divides the octave into 12 semitones of 100 cents each...
, an interval sometimes called the Holdrian comma.
History
Theoretical interest in this division goes back to antiquity. Ching Fang (78–37 BC), a Chinese music theorist, observed that a series of 53 just fifths (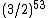 ) is very nearly equal to 31 octaves (
) is very nearly equal to 31 octaves (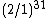 ). He calculated this difference with six-digit accuracy to be
). He calculated this difference with six-digit accuracy to be 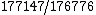 . Later the same observation was made by the mathematician and music theorist Nicholas Mercator
. Later the same observation was made by the mathematician and music theorist Nicholas MercatorNicholas Mercator
Nicholas Mercator , also known by his Germanic name Kauffmann, was a 17th-century mathematician....
(c. 1620–1687), who calculated this value precisely as
 , which is known as Mercator's comma. Mercator's comma is of such small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1/53 of that comma (≈ 0.0682 cent ≈ 1/315 syntonic comma
, which is known as Mercator's comma. Mercator's comma is of such small value to begin with (≈ 3.615 cents), but 53 equal temperament flattens each fifth by only 1/53 of that comma (≈ 0.0682 cent ≈ 1/315 syntonic commaSyntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
). Thus, 53 equal temperament is for all practical purposes equivalent to an extended Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
.
After Mercator, William Holder
William Holder
William Holder FRS was an English clergyman and music theorist of the 17th century. His most notable work was his widely known 1694 publication A Treatise on the Natural Grounds and Principles of Harmony.-Life:...
published a treatise in 1694 which pointed out that 53 equal temperament also very closely approximates the just major third (to within 1.4 cents), and consequently 53 equal temperament accommodates the intervals of 5-limit
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
just intonation very well. This property of 53-TET may have been known earlier; Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's unpublished manuscripts suggest that he had been aware of it as early as 1664–65.
Scale diagram
| Interval (cents) | 91 | 23 | 91 | 68 | 45 | 68 | 45 | 23 | 45 | 91 | 23 | 91 | 68 | 45 | 68 | 91 | 23 | 91 | 45 | 23 | 45 | |||||||||||||||||||||||
| Note name | C0 | C-1 | D1 | D0 | D-2 | E1 | E-1 | F2 | E-3 | F0 | F-1 | G1 | G0 | G-2 | A1 | A-1 | A-2 | B0 | B-1 | C2 | B-3 | C0 | ||||||||||||||||||||||
| Note (cents) | 0 | 91 | 113 | 204 | 272 | 317 | 385 | 430 | 453 | 498 | 589 | 611 | 702 | 770 | 815 | 883 | 974 | 996 | 1087 | 1132 | 1155 | 1200 | ||||||||||||||||||||||
Comparison to other scales
Because a distance of 31 steps in this scale is almost precisely equal to a justJust intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
, this scale can practically be considered a form of Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
that has been extended to 53 tones. As such the intervals available can have the same properties as any Pythagorean tuning, such as fifths that are (practically) pure, major thirds that are wide from just (about 81/64 opposed to the purer 5/4), and minor thirds that are conversely narrow (32/27 compared to 6/5).
However, unlike most Pythagorean forms of tuning, 53-TET contains additional intervals that are very close to just intonation. For instance, the interval of 17 steps is also a major third, but only 1.4 cents narrower than the very pure just interval 5/4. 53-TET is very good as an approximation to any interval in 5-limit just intonation.
| interval name | size (steps) | size (cents) | just ratio | just (cents) | error |
| perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
31 | 701.89 | 3:2 | 701.96 | −0.07 |
| diatonic tritone Tritone In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones... |
26 | 588.68 | 45:32 | 590.22 | −1.54 |
| septimal tritone Septimal tritone The lesser septimal tritone is the interval with ratio 7:5 . The inverse of that interval, the greater septimal tritone, is an interval with ratio 10:7... |
26 | 588.68 | 7:5 | 582.51 | +6.17 |
| classic tritone Tritone In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones... |
25 | 566.04 | 25:18 | 568.72 | −2.68 |
| undecimal tritone Tritone In classical music from Western culture, the tritone |tone]]) is traditionally defined as a musical interval composed of three whole tones. In a chromatic scale, each whole tone can be further divided into two semitones... |
24 | 543.40 | 11:8 | 551.32 | −7.92 |
| double diminished fifth | 24 | 543.40 | 512:375 | 539.10 | +4.30 |
| undecimal augmented fourth | 24 | 543.40 | 15:11 | 536.95 | +6.45 |
| acute fourth | 23 | 520.76 | 27:20 | 519.55 | +1.21 |
| perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
22 | 498.11 | 4:3 | 498.04 | +0.07 |
| grave fourth | 21 | 475.47 | 320:243 | 476.54 | −1.07 |
| septimal narrow fourth | 21 | 475.47 | 21:16 | 470.78 | +4.69 |
| classic augmented third | 20 | 452.83 | 125:96 | 456.99 | −4.16 |
| tridecimal augmented third | 20 | 452.83 | 13:10 | 454.21 | −1.38 |
| septimal major third Septimal major third In music, the septimal major third , also called the supermajor third and sometimes Bohlen–Pierce third is the musical interval exactly or approximately equal to a just 9:7 ratio of frequencies, or alternately 14:11. It is equal to 435 cents, sharper than a just major third by the septimal... |
19 | 430.19 | 9:7 | 435.08 | −4.90 |
| classic diminished fourth | 19 | 430.19 | 32:25 | 427.37 | +2.82 |
| ditone Ditone In music, a ditone is the interval 81:64, which is 407.82 cents. It is the major third in Pythagorean tuning. The ditone is evenly divisible by two major tones and is wider than a just major third by a syntonic comma... |
18 | 407.54 | 81:64 | 407.82 | −0.28 |
| just Just intonation In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series... major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
17 | 384.91 | 5:4 | 386.31 | −1.40 |
| grave major third | 16 | 362.26 | 100:81 | 364.80 | −2.54 |
| acute minor third | 15 | 339.62 | 243:200 | 337.15 | +2.47 |
| just minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... |
14 | 316.98 | 6:5 | 315.64 | +1.34 |
| semiditone | 13 | 294.34 | 32:27 | 294.13 | +0.21 |
| classic augmented second | 12 | 271.70 | 75:64 | 274.58 | −2.88 |
| septimal minor third Septimal minor third In music, the septimal minor third , also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5... |
12 | 271.70 | 7:6 | 266.87 | +4.83 |
| classic diminished third | 11 | 249.06 | 144:125 | 244.97 | +4.09 |
| diminished third | 10 | 226.41 | 256:225 | 223.46 | +2.95 |
| whole tone, major tone | 9 | 203.77 | 9:8 | 203.91 | −0.14 |
| whole tone, minor tone | 8 | 181.13 | 10:9 | 182.40 | −1.27 |
| neutral second Neutral second A neutral second or medium second is a musical interval wider than a minor second and narrower than a major second. Three distinct intervals may be termed neutral seconds:... , grave whole tone |
7 | 158.49 | 800:729 | 160.90 | −2.41 |
| neutral second, large limma | 6 | 135.85 | 27:25 | 133.24 | +2.61 |
| Pythagorean major semitone | 5 | 113.21 | 2187:2048 | 113.69 | −0.48 |
| just diatonic semitone | 5 | 113.21 | 16:15 | 111.73 | +1.48 |
| major limma Major limma Major limma is an interval with the ratio of 135:128, which is the difference between two major tones and a minor third. It is equal to about 92.18 cents.... |
4 | 90.57 | 135:128 | 92.18 | −1.61 |
| Pythagorean minor semitone | 4 | 90.57 | 256:243 | 90.22 | +0.34 |
| just chromatic semitone | 3 | 67.92 | 25:24 | 70.67 | −2.75 |
| just diesis Diesis In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents... |
2 | 45.28 | 128:125 | 41.06 | +4.22 |
| just syntonic comma Syntonic comma In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents... |
1 | 22.64 | 81:80 | 21.51 | +1.14 |
Theoretical properties
The 53-et tuning equates to the unison, or tempers out, the intervals 32805/32768, known as the schismaSchisma
In music, the schisma is the ratio between a Pythagorean comma and a syntonic comma and equals 32805:32768, which is 1.9537 cents...
, and 15625/15552, known as the kleisma
Kleisma
In music theory and tuning, the kleisma, or semicomma majeur, is a minute and barely perceptible comma type interval important to musical temperaments. It is the difference between six justly tuned minor thirds and one justly tuned tritave or perfect twelfth...
. These are both 5-limit intervals, involving only the primes 2, 3 and 5 in their factorization, and the fact that 53-et tempers out both characterizes it completely as a 5-limit temperament: it is the only regular temperament
Regular temperament
Regular temperament is any tempered system of musical tuning such that each frequency ratio is obtainable as a product of powers of a finite number of generators, or generating frequency ratios...
tempering out both of these intervals, or comma
Comma (music)
In music theory, a comma is a minute interval, the difference resulting from tuning one note two different ways. The word "comma" used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F tuned using the D-based Pythagorean tuning...
s, a fact which seems to have first been recognized by Japanese music theorist Shohé Tanaka
Shohé Tanaka
was a Japanese physicist, music theorist, and inventor. He graduated from Tokyo University in 1882 as a science student. On an imperial scholarship, he was sent to Germany for doctoral studies in 1884, together with Mori Ōgai...
. Because it tempers these out, 53-et can be used for both schismatic temperament
Schismatic temperament
The schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament or Helmholtz temperament.-Comparison with other tunings:...
, tempering out the schisma, and Hanson temperament (also called kleismic), tempering out the kleisma.
The interval of 7/4 is 4.8 cents sharp in 53-et, and using it for 7-limit harmony means that the septimal kleisma
Septimal kleisma
In music, the ratio 225/224 is called the septimal kleisma .It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 2 . That says that it is the amount that two major thirds of 5/4 and a septimal...
, the interval 225/224, is also tempered out.
Notation
Attempting to use standard notation, seven letter notes plus sharps/flats, can quickly become confusing. This is unlike the case with 19-ET19 equal temperament
In music, 19 equal temperament, called 19-TET, 19-EDO, or 19-ET, is the tempered scale derived by dividing the octave into 19 equal steps . Each step represents a frequency ratio of 21/19, or 63.16 cents...
and 31-ET
31 equal temperament
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET, 31-EDO , , is the tempered scale derived by dividing the octave into 31 equal-sized steps...
where there is little ambiguity. By not being meantone, it adds some problems that require more attention. Specifically, the major third is different from a ditone, two tones, each of which is two fifths minus an octave. Likewise, the minor third is different from a semiditone.
The fact that the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
is not tempered out means that things (notes, intervals) need to be defined more precisely.
Chords of 53 equal temperament
Standard musical notation can be used to denote 53 equal temperament; however, since it is a Pythagorean system, with nearly pure fifths, major and minor triads cannot be spelled in the same manner as in a meantoneMeantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
tuning. Instead, the major triads are chords like C-Fb-G, where the major third is a diminished fourth; this is the defining characteristic of schismatic temperament
Schismatic temperament
The schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament or Helmholtz temperament.-Comparison with other tunings:...
. Likewise, the minor triads are chords like C-D#-G. In 53-et the dominant seventh chord
Dominant seventh chord
In music theory, a dominant seventh chord, or major minor seventh chord,is a chord composed of a root, major third, perfect fifth, and minor seventh. It can be also viewed as a major triad with an additional minor seventh...
would be spelled C-Fb-G-Bb, but the otonal tetrad is C-Fb-G-Cbb, and C-Fb-G-A# is still another seventh chord. The utonal tetrad, the inversion of the otonal tetrad, is spelled C-D#-G-Gx.
Further septimal chords are the diminished triad, having the two forms C-D#-Gb and C-Fbb-Gb, the subminor triad, C-Fbb-G, the supermajor triad C-Dx-G, and corresponding tetrads C-Fbb-G-Bbb and C-Dx-G-A#. Since 53-et tempers out the septimal kleisma
Septimal kleisma
In music, the ratio 225/224 is called the septimal kleisma .It is a minute comma type interval of approximately 7.7 cents. Factoring it into primes gives 2−5 32 52 7−1, which can be rewritten 2−1 2 . That says that it is the amount that two major thirds of 5/4 and a septimal...
, the septimal kleisma augmented triad C-Fb-Bbb in its various inversions is also a chord of the system. So is the orwell tetrad, C-Fb-Dxx-Gx in its various inversions.
Music
In the 19th century, people began devising instruments in 53-et, with an eye to their use in playing near-just 5-limitLimit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
music. Such instruments were devised by RHM Bosanquet
Robert Holford Macdowall Bosanquet
Robert Holford Macdowall Bosanquet was an English scientist and music theorist, and brother of Admiral Sir Day Bosanquet, and philosopher Bernard Bosanquet....
and the American tuner James Paul White. Subsequently the temperament has seen occasional use by composers in the west, and has been used in Turkish music
Music of Turkey
The music of Turkey includes diverse elements ranging from Central Asian folk music and has many copies and references of Byzantine music, Greek music, Ottoman music, Persian music, Balkan music, as well as more modern European and American popular music influences...
as well; the Turkish composer Erol Sayan has employed it, following theoretical use of it by Turkish music theorist Kemal Ilerici. Arabic music, which for the most part bases its theory on quartertones, has also made some use of it; the Syrian violinist and music theorist Twfiq Al-Sabagh proposed that instead of an equal division of the octave into 24 parts a 24-note scale in 53-et should be used as the master
scale for Arabic music.
Croatian composer Josip Štolcer-Slavenski
Josip Štolcer-Slavenski
Josip Štolcer-Slavenski was a Yugoslav composer and professor at the Music Academy in Belgrade.-Early life:...
wrote one piece, which has never been published, which uses Bosanquet's Enharmonium
Robert Holford Macdowall Bosanquet
Robert Holford Macdowall Bosanquet was an English scientist and music theorist, and brother of Admiral Sir Day Bosanquet, and philosopher Bernard Bosanquet....
during its first movement, entitled Music for Natur-ton-system.
External links
- "Whisper Song in 53EDO" by Prent Rodgers, Podcast Bumper Music.
- PDF file: Larry Hanson. Development of a 53EDO Keyboard Layout, Anaphoria.com.
- "Algebra of Tonal Functions", Sonantometry. Tonal Functions as 53EDO grades.
- Barbieri, Patrizio. Enharmonic instruments and music, 1470–1900. (2008) Latina, Il Levante Libreria Editrice
- "Fractal Microtonal Music" by Jim Kukula.

