Zeckendorf's theorem
Encyclopedia
Belgium
Belgium , officially the Kingdom of Belgium, is a federal state in Western Europe. It is a founding member of the European Union and hosts the EU's headquarters, and those of several other major international organisations such as NATO.Belgium is also a member of, or affiliated to, many...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Edouard Zeckendorf
Edouard Zeckendorf
Edouard Zeckendorf was a Belgian doctor, army officer and mathematician. In mathematics, he is best known for his work on Fibonacci numbers and in particular for proving Zeckendorf's theorem....
, is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about the representation of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s as sums of Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
Zeckendorf's theorem states that every positive integer can be represented uniquely as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. More precisely, if N is any positive integer, there exist positive integers ci ≥ 2, with ci + 1 > ci + 1, such that
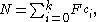
where Fn is the nth Fibonacci number. Such a sum is called the Zeckendorf representation of N. The Fibonacci coding
Fibonacci coding
In mathematics, Fibonacci coding is a universal code which encodes positive integers into binary code words. Each code word ends with "11" and contains no other instances of "11" before the end.-Definition:...
of N can be derived from its Zeckendorf representation.
For example, the Zeckendorf representation of 100 is
- 100 = 89 + 8 + 3.
There are other ways of representing 100 as the sum of Fibonacci numbers - for example
- 100 = 89 + 8 + 2 + 1
- 100 = 55 + 34 + 8 + 3
but these are not Zeckendorf representations because 1 and 2 are consecutive Fibonacci numbers, as are 34 and 55.
For any given positive integer, a representation that satisfies the conditions of Zeckendorf's theorem can be found by using a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
, choosing the largest possible Fibonacci number at each stage.
Proof
Zeckendorf's theorem has two parts:- Existence: every positive integer n has a Zeckendorf representation.
- Uniqueness: no positive integer n has two different Zeckendorf representations.
The first part of Zeckendorf's theorem (existence) can be proven by induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. For n = 1, 2, 3 it is clearly true (as these are Fibonacci numbers), for n = 4 we have 4 = 3 + 1. Now suppose each
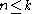has a Zeckendorf representation. If k + 1 is a Fibonacci number then we're done, else there exists j such that 
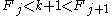. Now consider 
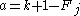. Since 
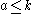, a has a Zeckendorf representation (by the induction hypothesis). At the same time, 
and since 
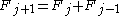(by definition of Fibonacci numbers), 
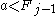, so the Zeckendorf representation of a does not contain 
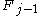. As a result, k + 1 can be represented as the sum of 
and the Zeckendorf representation of a.The second part of Zeckendorf's theorem (uniqueness) requires the following lemma:
- Lemma: The sum of any non-empty set of distinct, non-consecutive Fibonacci numbers whose largest member is
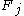is strictly less than the next largest Fibonacci number 
.
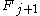The lemma can be proven by induction on j.
Now take two non-empty sets of distinct non-consecutive Fibonacci numbers S and T which have the same sum. Consider sets S' and T' which are equal to S and T from which the common elements have been removed (i.e.
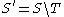and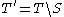 
. Since S and T had equal sum, and we have removed exactly the elements from 
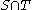from both sets, S' and T' must have the same sum as well.Now we will show by contradiction that at least one of S' and T' is empty. Assume the contrary, i.e. that S' and T' are both non-empty and let the largest member of S' be
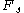and the largest member of T' be 
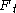. Because S' and T' contain no common elements, 
. Without loss of generalityWithout loss of generality
Without loss of generality is a frequently used expression in mathematics...
, suppose
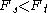. Then by the lemma, the sum of S' is strictly less than 
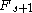and so is strictly less than 
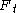, whereas the sum of T' is clearly at least 
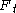. This contradicts the fact that S' and T' have the same sum, and we can conclude that either S' or T' must be empty.Now assume (again without loss of generality) that S' is empty. Then S' has sum 0, and so must T'. But since T' can only contain positive integers, it must be empty too. To conclude:
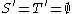which implies 
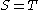, proving that each Zeckendorf representation is unique.Fibonacci multiplication
One can define the following operation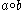
on natural numbers a, b: given the Zeckendorf representations
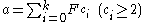and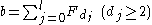 
we define the Fibonacci product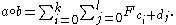 
For example, the Zeckendorf representation of 2 is
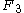, and the Zeckendorf representation of 4 is 
(
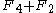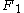is disallowed from representations), so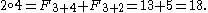 
Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
proved the surprising fact that this operation is associative.
Representation with negafibonacci numbers
The Fibonacci sequence can be extended to negative index n using the re-arranged recurrence relation
which yields the sequence of "negafibonacci" numbers satisfying
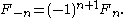
Any integer can be uniquely represented as a sum of negafibonacci numbers in which no two consecutive negafibonacci numbers are used. For example:
- -11 = F-4 + F-6 = (-3) + (-8)
- 12 = F-2 + F-7 = (-1) + 13
- 24 = F-1 + F-4 + F-6 + F-9 = 1 + (-3) + (-8) + 34
- -43 = F-2 + F-7 + F-10 = (-1) + 13 + (-55)
- 0 is represented by the empty sumEmpty sumIn mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
.
Note that 0 = F-1 + F-2, for example, so the uniqueness of the representation does depend on the condition that no two consecutive negafibonacci numbers are used.
This gives a system
NegaFibonacci coding
In mathematics, negaFibonacci coding is a universal code which encodes integers into binary code words. It is similar to Fibonacci coding, except that it allows both positive and negative integers to be represented. All codes end with "11" and have no "11" before the end...
of coding integers, similar to the representation of Zeckendorf's theorem. In the string representing the integer x, the nth digit is 1 if Fn appears in the sum that represents x; that digit is 0 otherwise. For example, 24 may be represented by the string 100101001, which has the digit 1 in places 9, 6, 4, and 1, because 24 = F-1 + F-4 + F-6 + F-9. The integer x is represented by a string of odd length if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
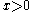.External links
- Zeckendorf's theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...