Wirtinger inequality (2-forms)
Encyclopedia
In mathematics, the Wirtinger inequality for 2-forms, named after Wilhelm Wirtinger
, states that the exterior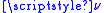
th power of the standard symplectic form ω, when evaluated on a simple (decomposable) 
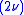-vector ζ of unit volume, is bounded above by 
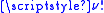. In other words,
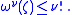
Wilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
, states that the exterior
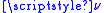th power of the standard symplectic form ω, when evaluated on a simple (decomposable) 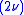-vector ζ of unit volume, is bounded above by 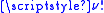. In other words,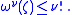See also
- 2-form
- Gromov's inequality for complex projective space
- Systolic geometry