Wigner's theorem
Encyclopedia
Wigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics
. The theorem specifies how physical symmetries such as rotations, translations, and CPT
act on the Hilbert space of states.
According to the theorem, any symmetry acts as an unitary
or antiunitary transformation in the Hilbert space. More precisely, it states that a surjective map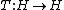
on a complex Hilbert space
that satisfies
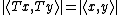
for all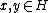
has the form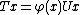 
for all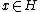
, where 
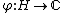has modulus
one and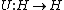
is either unitary or antiunitary.
and quantum field theory
, the quantum state that characterizes one or more particles or fields is a vector (ket
) in a complex Hilbert space. Any symmetry operation, for example "translate all particles and fields forward in time by five seconds", or "Lorentz transform all particles and fields by a 5 m/s boost in the x direction", corresponds to an operator T on that Hilbert space. This operator T must be bijective because every quantum state must have a unique corresponding transformed state and vice-versa. Also, the probability of finding a system in state
when it is initially in state 
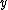is given by 
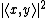. Since T is a symmetry operation, the probability of finding the system in state 
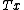when it is initially in state 
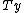must be the same; therefore 
. It follows that T satisfies the hypotheses of Wigner's theorem.
Thus, according to Wigner's theorem, T is either unitary or anti-unitary. In the two examples above (time translations and Lorentz boosts), T corresponds to a unitary symmetry operator. The time-reversal symmetry operator is a famous example of an anti-unitary symmetry operator.
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
. The theorem specifies how physical symmetries such as rotations, translations, and CPT
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
act on the Hilbert space of states.
According to the theorem, any symmetry acts as an unitary
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
or antiunitary transformation in the Hilbert space. More precisely, it states that a surjective map
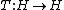on a complex Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
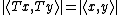
that satisfiesfor all
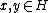has the form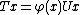 for all
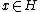, where 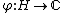has modulusAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
one and
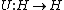is either unitary or antiunitary.Symmetry in quantum mechanics
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the quantum state that characterizes one or more particles or fields is a vector (ket
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
) in a complex Hilbert space. Any symmetry operation, for example "translate all particles and fields forward in time by five seconds", or "Lorentz transform all particles and fields by a 5 m/s boost in the x direction", corresponds to an operator T on that Hilbert space. This operator T must be bijective because every quantum state must have a unique corresponding transformed state and vice-versa. Also, the probability of finding a system in state
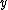when it is initially in state is given by 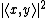. Since T is a symmetry operation, the probability of finding the system in state 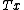when it is initially in state 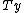must be the same; therefore . It follows that T satisfies the hypotheses of Wigner's theorem.Thus, according to Wigner's theorem, T is either unitary or anti-unitary. In the two examples above (time translations and Lorentz boosts), T corresponds to a unitary symmetry operator. The time-reversal symmetry operator is a famous example of an anti-unitary symmetry operator.