
Weierstrass–Erdmann condition
Encyclopedia
The Weierstrass–Erdmann condition is a technical tool from the calculus of variations
. This condition gives the sufficient conditions for an extremal to have a corner.
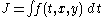 , the partial derivative
, the partial derivative 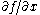 must be continuous at a corner T. That is, if one takes the limit of partials on both sides of the corner as one approaches the corner T, the result must be the same answer.
must be continuous at a corner T. That is, if one takes the limit of partials on both sides of the corner as one approaches the corner T, the result must be the same answer.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. This condition gives the sufficient conditions for an extremal to have a corner.
Conditions
The condition says that, along a piecewise smooth extremal x(t) (i.e. an extremal which is smooth except at a finite number of corners) for an integral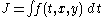 , the partial derivative
, the partial derivative 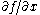 must be continuous at a corner T. That is, if one takes the limit of partials on both sides of the corner as one approaches the corner T, the result must be the same answer.
must be continuous at a corner T. That is, if one takes the limit of partials on both sides of the corner as one approaches the corner T, the result must be the same answer.
