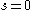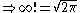Wallis product
Encyclopedia
In mathematics
, Wallis' product for π
, written down in 1655 by John Wallis, states that
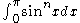for even and odd values of n, and noting that for large n, increasing n by 1 makes little change. Since infinitesimal calculus
as we know it did not yet exist then, and mathematical analysis
sufficient to discuss the convergence issue was inadequate, this was a harder piece of research than it sounds with hindsight, and more tentative. Wallis's product is, in retrospect, an easy corollary of the later Euler formula for the sine function.
Let x = π/2:
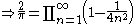
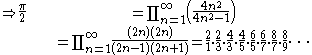
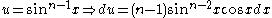
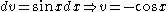
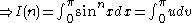
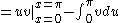
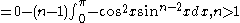
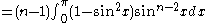
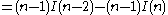
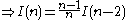
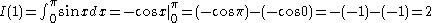
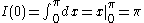
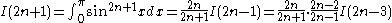
Repeating the process,
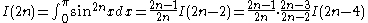
Repeating the process,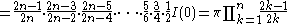
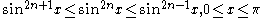
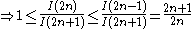
By the squeeze theorem
,
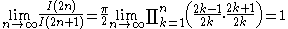
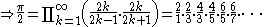
for n! asserts that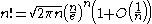
as n → ∞. Consider now the finite approximations to the Wallis product, obtained by taking the first k terms in the product
:
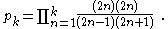
pk can be written as
Substituting Stirling's approximation in this expression (both for k! and (2k)!) one can deduce (after a short calculation) that pk converges to π/2 as k → ∞.
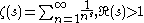
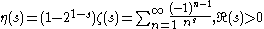
Applying an Euler transform to the latter series, the following is obtained: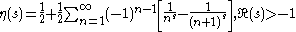
,
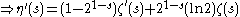
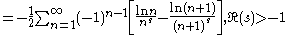
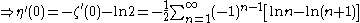
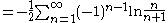
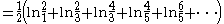
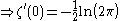
Plugging in
gives:
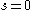
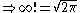
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Wallis' product for π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, written down in 1655 by John Wallis, states that
Derivation
Wallis derived his product as it is done in calculus books today, by comparing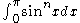 for even and odd values of n, and noting that for large n, increasing n by 1 makes little change. Since infinitesimal calculusInfinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
as we know it did not yet exist then, and mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
sufficient to discuss the convergence issue was inadequate, this was a harder piece of research than it sounds with hindsight, and more tentative. Wallis's product is, in retrospect, an easy corollary of the later Euler formula for the sine function.
Proof using Euler's infinite product for the sine function
Let x = π/2:
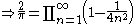
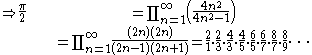
Proof using integral
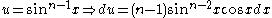
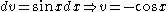
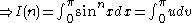
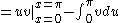
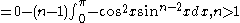
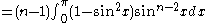
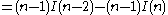
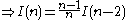
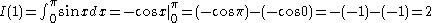
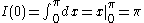
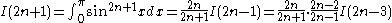
Let:Repeating the process,
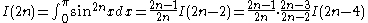
Repeating the process,
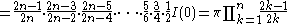
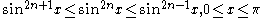
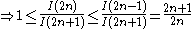
By the squeeze theorem
Squeeze theorem
In calculus, the squeeze theorem is a theorem regarding the limit of a function....
,
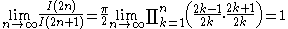
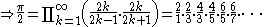
Relation to Stirling's approximation
Stirling's approximationStirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
for n! asserts that
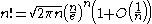
as n → ∞. Consider now the finite approximations to the Wallis product, obtained by taking the first k terms in the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
:
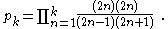
pk can be written as
Substituting Stirling's approximation in this expression (both for k! and (2k)!) one can deduce (after a short calculation) that pk converges to π/2 as k → ∞.
ζ'(0)
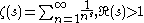
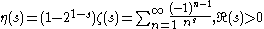
The Riemann zeta function and the Dirichlet eta function can be defined:Applying an Euler transform to the latter series, the following is obtained:
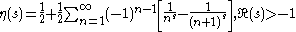
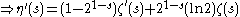
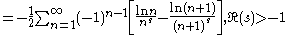
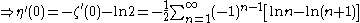
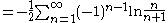
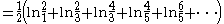
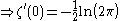
Infinity factorial
Using zeta function regularizationZeta function regularization
In mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators...
,
Plugging in
gives: