
Vanna Volga
Encyclopedia
The Vanna-Volga method is a technique for pricing first-generation exotic option
s in FX
derivatives
.
It consists in adjusting the Black–Scholes theoretical value (BSTV)
by the cost of a portfolio which hedges three main risks
associated to the volatility of the option: the Vega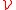 , the Vanna
, the Vanna
and the Volga. The Vanna is the sensitivity of the Vega with
respect to a change in the spot FX rate:
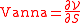 .
.
Similarly, the Volga is the sensitivity
of the Vega with respect to a change of the implied volatility
 :
:
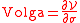 .
.
If we consider a smile volatility surface
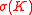 with ATM strike
with ATM strike 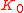 , ATM volatility
, ATM volatility 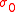 , and where
, and where  are the 25-Delta
are the 25-Delta
call/put strikes (obtained by solving the equations and
and  where
where 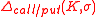 denotes the
denotes the
Black–Scholes Delta sensitivity
) then the hedging portfolio
will be composed of the at-the-money (ATM), risk-reversal (RR) and butterfly (BF)
strategies:
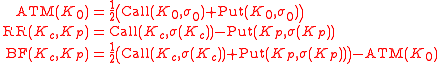
with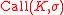 the Black–Scholes price of a call option (similarly for the put).
the Black–Scholes price of a call option (similarly for the put).
The simplest formulation of the Vanna-Volga method suggests that the
Vanna-Volga price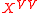 of an exotic instrument
of an exotic instrument  is
is
given by
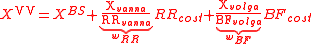
where by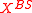 denotes the Black–Scholes price of the
denotes the Black–Scholes price of the
exotic and the Greeks are calculated with ATM volatility and
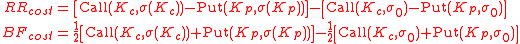
These quantities represent a smile cost, namely the
difference between the price computed with/without including the
smile effect.
The rationale behind the above formulation of the Vanna-Volga price is that one can extract
the smile cost of an exotic option by measuring the
smile cost of a portfolio designed to hedge its Vanna and
Volga risks. The reason why one chooses the strategies BF and RR
to do this is because they are liquid FX instruments and they
carry mainly Volga, and respectively Vanna risks. The weighting
factors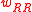 and
and 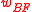 represent
represent
respectively the amount of RR needed to replicate the option's
Vanna, and the amount of BF needed to replicate the option's
Volga. The above approach ignores the small (but non-zero)
fraction of Volga carried by the RR and the small fraction of
Vanna carried by the BF. It further neglects the cost of hedging
the Vega risk. This has led to a more general formulation of the
Vanna-Volga method in which one considers that within the Black–Scholes
assumptions the exotic option's Vega, Vanna and Volga can be
replicated by the weighted sum of three instruments:

where the weightings are obtained by solving the system:

with
 ,
,
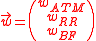 ,
,
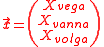
Given this replication, the Vanna-Volga method adjusts the BS
price of an exotic option by the smile cost of the above
weighted sum (note that the ATM smile cost is zero by
construction):

where
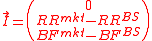
and
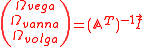
The quantities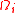 can be interpreted as the
can be interpreted as the
market prices attached to a unit amount of Vega, Vanna and Volga,
respectively. The resulting correction, however, typically turns
out to be too large. Market practitioners thus modify
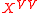 to
to

The Vega contribution turns out to be
several orders of magnitude smaller than the Vanna and Volga terms
in all practical situations, hence one neglects it.
The terms and
and  are put in by-hand and represent factors that ensure the correct behaviour of the price of an exotic option near a barrier:
are put in by-hand and represent factors that ensure the correct behaviour of the price of an exotic option near a barrier:
as the knock-out barrier level of an option
of an option
is gradually moved toward the spot level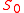 , the BSTV price of a
, the BSTV price of a
knock-out option must be a monotonically decreasing function, converging
to zero exactly at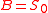 . Since the Vanna-Volga method is a
. Since the Vanna-Volga method is a
simple rule-of-thumb and not a rigorous model, there is no
guarantee that this will be a priori the case. The attenuation factors are of a different from for the Vanna or the Volga
of an instrument. This is because for barrier values close to the spot they behave differently: the Vanna becomes large while,
on the contrary, the Volga becomes small. Hence the
attenuation factors take the form:
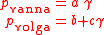
where represents some measure of the barrier(s)
represents some measure of the barrier(s)
vicinity to the spot with the features
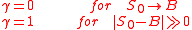
The coefficients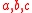 are found through calibration of the model to ensure that it reproduces the vanilla smile. Good candidates for
are found through calibration of the model to ensure that it reproduces the vanilla smile. Good candidates for  that ensure the appropriate behaviour close to the barriers are the survival probability and the expected first exit time. Both of these quantities offer the desirable property that they vanish close to a barrier.
that ensure the appropriate behaviour close to the barriers are the survival probability and the expected first exit time. Both of these quantities offer the desirable property that they vanish close to a barrier.
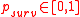 refers to the
refers to the
probability that the spot does not touch one or more barrier
levels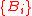 . For example, for a single barrier option we have
. For example, for a single barrier option we have
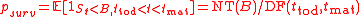
where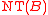 is the value of a no-touch option and
is the value of a no-touch option and 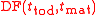 the discount factor between today and maturity. Similarly, for options with two barriers
the discount factor between today and maturity. Similarly, for options with two barriers
the survival probability is given through the undiscounted value
of a double-no-touch option.
the future when the spot is expected to exit a barrier zone before
maturity, and (ii) maturity, if the spot has not hit any of the
barrier levels up to maturity. That is, if we denote the FET by
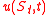 then
then 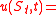 min
min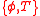 where
where
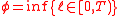 such that
such that  or
or
 where
where 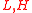 are the 'low' vs 'high' barrier levels and
are the 'low' vs 'high' barrier levels and
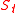 the spot of today.
the spot of today.
The first-exit time is the solution of the following PDE
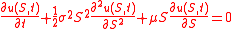
This equation is solved backwards
in time starting from the terminal condition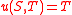 where
where  is the time to maturity and
is the time to maturity and
boundary conditions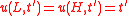 . In case of a single
. In case of a single
barrier option we use the same PDE with either or
or  . The parameter
. The parameter  represents the risk-neutral drift of the underlying stochastic process.
represents the risk-neutral drift of the underlying stochastic process.
Exotic option
In finance, an exotic option is a derivative which has features making it more complex than commonly traded products . These products are usually traded over-the-counter , or are embedded in structured notes....
s in FX
Foreign exchange market
The foreign exchange market is a global, worldwide decentralized financial market for trading currencies. Financial centers around the world function as anchors of trading between a wide range of different types of buyers and sellers around the clock, with the exception of weekends...
derivatives
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
.
It consists in adjusting the Black–Scholes theoretical value (BSTV)
by the cost of a portfolio which hedges three main risks
associated to the volatility of the option: the Vega
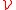 , the Vanna
, the Vannaand the Volga. The Vanna is the sensitivity of the Vega with
respect to a change in the spot FX rate:
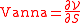 .
.Similarly, the Volga is the sensitivity
of the Vega with respect to a change of the implied volatility
 :
: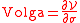 .
.If we consider a smile volatility surface
Volatility Smile
In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
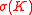 with ATM strike
with ATM strike 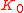 , ATM volatility
, ATM volatility 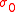 , and where
, and where  are the 25-Delta
are the 25-Deltacall/put strikes (obtained by solving the equations
 and
and  where
where 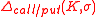 denotes the
denotes theBlack–Scholes Delta sensitivity
Greeks (finance)
In mathematical finance, the Greeks are the quantities representing the sensitivities of the price of derivatives such as options to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of...
) then the hedging portfolio
will be composed of the at-the-money (ATM), risk-reversal (RR) and butterfly (BF)
strategies:
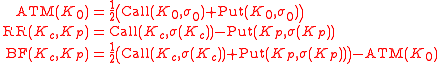
with
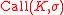 the Black–Scholes price of a call option (similarly for the put).
the Black–Scholes price of a call option (similarly for the put).The simplest formulation of the Vanna-Volga method suggests that the
Vanna-Volga price
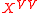 of an exotic instrument
of an exotic instrument  is
isgiven by
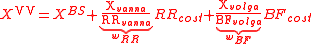
where by
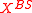 denotes the Black–Scholes price of the
denotes the Black–Scholes price of theexotic and the Greeks are calculated with ATM volatility and
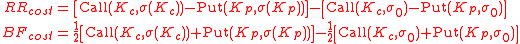
These quantities represent a smile cost, namely the
difference between the price computed with/without including the
smile effect.
The rationale behind the above formulation of the Vanna-Volga price is that one can extract
the smile cost of an exotic option by measuring the
smile cost of a portfolio designed to hedge its Vanna and
Volga risks. The reason why one chooses the strategies BF and RR
to do this is because they are liquid FX instruments and they
carry mainly Volga, and respectively Vanna risks. The weighting
factors
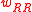 and
and 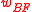 represent
representrespectively the amount of RR needed to replicate the option's
Vanna, and the amount of BF needed to replicate the option's
Volga. The above approach ignores the small (but non-zero)
fraction of Volga carried by the RR and the small fraction of
Vanna carried by the BF. It further neglects the cost of hedging
the Vega risk. This has led to a more general formulation of the
Vanna-Volga method in which one considers that within the Black–Scholes
assumptions the exotic option's Vega, Vanna and Volga can be
replicated by the weighted sum of three instruments:

where the weightings are obtained by solving the system:

with
 ,
,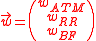 ,
,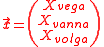
Given this replication, the Vanna-Volga method adjusts the BS
price of an exotic option by the smile cost of the above
weighted sum (note that the ATM smile cost is zero by
construction):

where
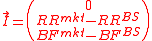
and
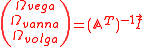
The quantities
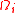 can be interpreted as the
can be interpreted as themarket prices attached to a unit amount of Vega, Vanna and Volga,
respectively. The resulting correction, however, typically turns
out to be too large. Market practitioners thus modify
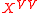 to
to
The Vega contribution turns out to be
several orders of magnitude smaller than the Vanna and Volga terms
in all practical situations, hence one neglects it.
The terms
 and
and  are put in by-hand and represent factors that ensure the correct behaviour of the price of an exotic option near a barrier:
are put in by-hand and represent factors that ensure the correct behaviour of the price of an exotic option near a barrier:as the knock-out barrier level
 of an option
of an optionis gradually moved toward the spot level
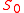 , the BSTV price of a
, the BSTV price of aknock-out option must be a monotonically decreasing function, converging
to zero exactly at
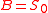 . Since the Vanna-Volga method is a
. Since the Vanna-Volga method is asimple rule-of-thumb and not a rigorous model, there is no
guarantee that this will be a priori the case. The attenuation factors are of a different from for the Vanna or the Volga
of an instrument. This is because for barrier values close to the spot they behave differently: the Vanna becomes large while,
on the contrary, the Volga becomes small. Hence the
attenuation factors take the form:
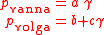
where
 represents some measure of the barrier(s)
represents some measure of the barrier(s)vicinity to the spot with the features
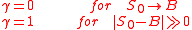
The coefficients
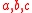 are found through calibration of the model to ensure that it reproduces the vanilla smile. Good candidates for
are found through calibration of the model to ensure that it reproduces the vanilla smile. Good candidates for  that ensure the appropriate behaviour close to the barriers are the survival probability and the expected first exit time. Both of these quantities offer the desirable property that they vanish close to a barrier.
that ensure the appropriate behaviour close to the barriers are the survival probability and the expected first exit time. Both of these quantities offer the desirable property that they vanish close to a barrier.Survival Probability
The survival probability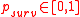 refers to the
refers to theprobability that the spot does not touch one or more barrier
levels
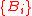 . For example, for a single barrier option we have
. For example, for a single barrier option we have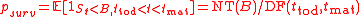
where
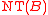 is the value of a no-touch option and
is the value of a no-touch option and 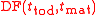 the discount factor between today and maturity. Similarly, for options with two barriers
the discount factor between today and maturity. Similarly, for options with two barriersthe survival probability is given through the undiscounted value
of a double-no-touch option.
First-exit time
The first exit time (FET) is the minimum between: (i) the time inthe future when the spot is expected to exit a barrier zone before
maturity, and (ii) maturity, if the spot has not hit any of the
barrier levels up to maturity. That is, if we denote the FET by
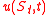 then
then 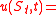 min
min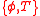 where
where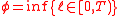 such that
such that  or
or where
where 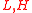 are the 'low' vs 'high' barrier levels and
are the 'low' vs 'high' barrier levels and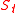 the spot of today.
the spot of today.The first-exit time is the solution of the following PDE
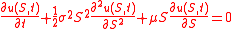
This equation is solved backwards
in time starting from the terminal condition
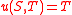 where
where  is the time to maturity and
is the time to maturity andboundary conditions
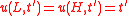 . In case of a single
. In case of a singlebarrier option we use the same PDE with either
 or
or  . The parameter
. The parameter  represents the risk-neutral drift of the underlying stochastic process.
represents the risk-neutral drift of the underlying stochastic process.

