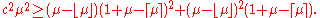Van Houtum distribution
Encyclopedia
In probability theory
and statistics
, the Van Houtum distribution is a discrete probability distribution named after prof. Geert-Jan van Houtum. It can be characterized by saying that all values of a finite set of possible values are equally probable, except for the smallest and largest element of this set. Since the Van Houtum distribution is a generalization of the discrete uniform distribution, i.e. it is uniform except possibly at its boundaries, it is sometimes also referred to as quasi-uniform.
It is regularly the case that the only available information concerning some discrete random variable variable are its first two moments. The Van Houtum distribution can be used to fit a distribution with finite support on these moments.
A simple example of the Van Houtum distribution arises when throwing a loaded dice which has been tampered with to land on a 6 twice as often as on a 1. The possible values of the sample space are 1, 2, 3, 4, 5 and 6. Each time the die is thrown, the probability of throwing a 2, 3, 4 or 5 is 1/6; the probability of a 1 is 1/18 and the probability of throwing a 6 is 2/9.
U has a Van Houtum (a, b, pa, pb) distribution if its probability mass function
is
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Van Houtum distribution is a discrete probability distribution named after prof. Geert-Jan van Houtum. It can be characterized by saying that all values of a finite set of possible values are equally probable, except for the smallest and largest element of this set. Since the Van Houtum distribution is a generalization of the discrete uniform distribution, i.e. it is uniform except possibly at its boundaries, it is sometimes also referred to as quasi-uniform.
It is regularly the case that the only available information concerning some discrete random variable variable are its first two moments. The Van Houtum distribution can be used to fit a distribution with finite support on these moments.
A simple example of the Van Houtum distribution arises when throwing a loaded dice which has been tampered with to land on a 6 twice as often as on a 1. The possible values of the sample space are 1, 2, 3, 4, 5 and 6. Each time the die is thrown, the probability of throwing a 2, 3, 4 or 5 is 1/6; the probability of a 1 is 1/18 and the probability of throwing a 6 is 2/9.
Probability mass function
A random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
U has a Van Houtum (a, b, pa, pb) distribution if its probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
is
-
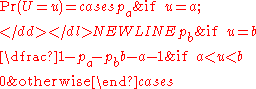
Fitting procedure
Suppose a random variable
has mean 
and squared coefficient of variationCoefficient of variationIn probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
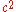. Let 
be a Van Houtum distributed random variable. Then the first two moments of 
match the first two moments of 
if 
, 
, 
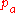and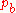 
are chosen such that:
-
There does not exist a Van Houtum distribution for every combination of
and 
. By using the fact that for any real mean 
the discrete distribution on the integers that has minimal variance is concentrated on the integers 
and 
, it is easy to verify that a Van Houtum distribution (or indeed any discrete distribution on the integers) can only be fitted on the first two moments if
-
-
