
Van Emde Boas tree
Encyclopedia
| van Emde Boas tree | |
|---|---|
| Type | Non-binary tree |
| Invented | 1977 |
| Invented by | Peter van Emde Boas |
| Asymptotic complexity in big O notation Big O notation In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or... |
|
| Space | O(M) |
| Search | O(log log M) |
| Insert | O(log log M) |
| Delete | O(log log M) |
A van Emde Boas tree (or van Emde Boas priority queue), also known as a vEB tree, is a tree data structure which implements an associative array
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
with m-bit integer keys. It performs all operations in O(log m) time. Notice that m is the size of the keys — therefore O(log m) is O(log log n) in a tree where every key below n is set, exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
better than a full self-balancing binary search tree
Self-balancing binary search tree
In computer science, a self-balancing binary search tree is any node based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions....
. They also have good space efficiency when they contain a large number of elements, as discussed below. They were invented by a team led by Peter van Emde Boas in 1977.
Supported operations
The operations supported by a vEB tree are those of an ordered associative arrayAssociative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
, which includes the usual associative array operations along with two more order operations, FindNext and FindPrevious:
- Insert: insert a key/value pair with an m-bit key
- Delete: remove the key/value pair with a given key
- Lookup: find the value associated with a given key
- FindNext: find the key/value pair with the smallest key at least a given k
- FindPrevious: find the key/value pair with the largest key at most a given k
How it works
For the sake of simplicity, let log2 m = k for some integer k. Define M=2m. A vEB tree T over the universe {0,...,M-1} has a root node that stores an array T.children of length M1/2. T.children[i] is a pointer to a vEB tree that is responsible for the values {iM1/2,...,(i+1)M1/2-1}. Additionally, T stores two values T.min and T.max as well as an auxiliary vEB tree T.aux.Data is stored in a vEB tree as follows: The smallest value currently in the tree is stored in T.min and largest value is stored in T.max. These two values are not stored anywhere else in the vEB tree. If T is empty then we use the convention that T.max=-1 and T.min=M. Any other value x is stored in the subtree T.children[i] where
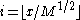 . The auxiliary tree T.aux keeps track of which children are non-empty, so T.aux contains the value j if and only if T.children[j] is non-empty.
. The auxiliary tree T.aux keeps track of which children are non-empty, so T.aux contains the value j if and only if T.children[j] is non-empty.FindNext
The operation FindNext(T, x) that searches for the successor of an element x in a vEB tree proceeds as follows: If x≤T.min then the search is complete, and the answer is T.min. If x>T.max then the next element does not exist, return M. Otherwise, let i=x/M1/2. If x≤T.children[i].max then the value being searched for is contained in T.children[i] so the search proceeds recursively in T.children[i]. Otherwise, We search for the value i in T.aux. This gives us the index j of the first subtree that contains an element larger than x. The algorithm then returns T.children[j].min. The element found on the children level needs to be composed with the high bits to form a complete next element.
FindNext(T, x)
if (x <= T.min)
return T.min
if (x > T.max) //no next element
return M
i = floor(x/sqrt(M))
lo = x % sqrt(M)
hi = x - lo
if (lo <= T.children[i].max)
return hi + FindNext(T.children[i], lo)
return hi + T.children[FindNext(T.aux,i+1)].min
Note that, in any case, the algorithm performs O(1) work and then possibly recurses on a subtree over a universe of size M1/2 (an m/2 bit universe). This gives a recurrence for the running time of T(m)=T(m/2) + O(1), which resolves to O(log m) = O(log log M).
Insert
The call Insert(T, x) that inserts a value x into a vEB tree T operates as follows:If T is empty then we set T.min = T.max = x and we are done.
Otherwise, if x<T.min then we insert T.min into the subtree i responsible for T.min and then set T.min = x. If T.children[i] was previously empty, then we also insert i into T.aux
Otherwise, if x>T.max then we insert T.max into the subtree i responsible for T.max and then set T.max = x. If T.children[i] was previously empty, then we also insert i into T.aux
Otherwise, T.min< x < T.max so we insert x into the subtree i responsible for x. If T.children[i] was previously empty, then we also insert i into T.aux.
In code:
Insert(T, x)
if (T.min > T.max) // T is empty
T.min = T.max = x;
return
if (T.min = T.max)
if (x < T.min)
T.min = x;
if (x > T.max)
T.max = x;
return
if (x < T.min)
swap(x, T.min)
if (x > T.max)
swap(x, T.max)
i = x/sqrt(M)
Insert(T.children[i], x % sqrt(M))
if (T.children[i].min = T.children[i].max)
Insert(T.aux, i)
The key to the efficiency of this procedure is that inserting an element into an empty vEB tree takes O(1) time. So, even though the algorithm sometimes makes two recursive calls, this only occurs when the first recursive call was into an empty subtree. This gives the same running time recurrence of T(m)=T(m/2) + O(1) as before.
Delete
Deletion from vEB trees is the trickiest of the operations. The call Delete(T, x) that deletes a value x from a vEB tree T operates as follows:If T.min = T.max = x then x is the only element stored in the tree and we set T.min = M and T.max = -1 to indicate that the tree is empty.
Otherwise, if x = T.min then we need to find the second-smallest value y in the vEB tree, delete it from its current location, and set T.min=y. The second-smallest value y is either T.max or T.children[T.aux.min].min, so it can be found in 'O'(1) time. In the latter case we delete y from the subtree that contains it.
Similarly, if x = T.max then we need to find the second-largest value y in the vEB tree, delete it from its current location, and set T.max=y. The second-largest value y is either T.min or T.children[T.aux.max].max, so it can be found in 'O'(1) time. In the latter case, we delete y from the subtree that contains it.
In case where x is not T.min or T.max, and T has no other elements, we know x is not in T and return without further operations.
Otherwise, we have the typical case where x≠T.min and x≠T.max. In this case we delete x from the subtree T.children[i] that contains x.
In any of the above cases, if we delete the last element x or y from any subtree T.children[i] then we also delete i from T.aux
In code:
Delete(T, x)
if (T.minT.max
x)
T.min = M
T.max = -1
return
if (xT.min)
T.max)
if (T.aux is empty)
T.min = T.max
return
else
x = T.children[T.aux.min].min
T.min = x
if (x
if (T.aux is empty)
T.max = T.min
return
else
x = T.children[T.aux.max].max
T.max = x
if (T.aux is empty)
return
i = floor(x/sqrt(M))
Delete(T.children[i], x%sqrt(M))
if (T.children[i] is empty)
Delete(T.aux, i)
Again, the efficiency of this procedure hinges on the fact that deleting from a vEB tree that contains only one element takes only constant time. In particular, the last line of code only executes if x was the only element in T.children[i] prior to the deletion.
Discussion
The assumption that log m is an integer is unnecessary. The operations x/sqrt(m) and x%sqrt(m) can be replaced by taking only higher-order ceil(m/2) and the lower-order floor(m/2) bits of x, respectively. On any existing machine, this is more efficient than division or remainder computations.The implementation described above uses pointers and occupies a total space of
 .
.This can be seen as follows. The recurrence is
 .
.Resolving that would lead to
 .
.One can, fortunately, also show that
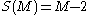 by induction.
by induction.In practical implementations, especially on machines with shift-by-k and find first zero instructions, performance can further be improved by switching to a bit array once m equal to the word size (or a small multiple thereof) is reached. Since all operations on a single word are constant time, this does not affect the asymptotic performance, but it does avoid the majority of the pointer storage and several pointer dereferences, achieving a significant practical savings in time and space with this trick.
An obvious optimization of vEB trees is to discard empty subtrees. This makes vEB trees quite compact when they contain many elements, because no subtrees are created until something needs to be added to them. Initially, each element added creates about log(m) new trees containing about m/2 pointers all together. As the tree grows, more and more subtrees are reused, especially the larger ones. In a full tree of 2m elements, only O(2m) space is used. Moreover, unlike a binary search tree, most of this space is being used to store data: even for billions of elements, the pointers in a full vEB tree number in the thousands.
However, for small trees the overhead associated with vEB trees is enormous: on the order of 2m/2. This is one reason why they are not popular in practice. One way of addressing this limitation is to use only a fixed number of bits per level, which results in a trie
Trie
In computer science, a trie, or prefix tree, is an ordered tree data structure that is used to store an associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the...
. Other structures, including y-fast trie
Y-fast trie
In computer science, a y-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O, using O space, where n is the number of stored values and M is the maximum value in the domain...
s and x-fast trie
X-fast trie
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O, using O space, where n is the number of stored values and M is the maximum value in the domain...
s have been proposed that have comparable update and query times but use only O(n) or O(n log M) space where n is the number of elements stored in the data structure.

