
VEGAS algorithm
Encyclopedia
The VEGAS algorithm, due to G. P. Lepage, is a method for reducing error
in Monte Carlo simulations by using a known or approximate probability distribution
function to concentrate the search in those areas of the graph that make the greatest contribution to the final integral
.
The VEGAS algorithm is based on importance sampling
. It samples points from the probability distribution described by the function |f|, so that the points are concentrated in the regions that make the largest contribution to the integral.
In general, if the Monte Carlo integral of f is sampled with points distributed according to a probability distribution described by the function g, we obtain an estimate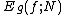 ,
,
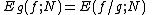
where is the Monte Carlo estimate of the integral of f,
is the Monte Carlo estimate of the integral of f,
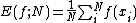
for N randomly distributed points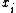 .
.
The variance
of the new estimate is then
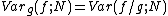
where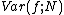 is the variance of the original estimate,
is the variance of the original estimate, 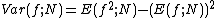 .
.
If the probability distribution is chosen as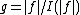 then it can be shown that the variance
then it can be shown that the variance 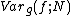 vanishes, and the error in the estimate will be zero. In practice it is not possible to sample from the exact distribution g for an arbitrary function, so importance sampling algorithms aim to produce efficient approximations to the desired distribution.
vanishes, and the error in the estimate will be zero. In practice it is not possible to sample from the exact distribution g for an arbitrary function, so importance sampling algorithms aim to produce efficient approximations to the desired distribution.
The VEGAS algorithm approximates the exact distribution by making a number of passes over the integration region while histogramming the function f. Each histogram is used to define a sampling distribution for the next pass. Asymptotically this procedure converges to the desired distribution. In order to avoid the number of histogram bins growing like the probability distribution is approximated by a separable function:
the probability distribution is approximated by a separable function: 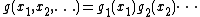 so that the number of bins required is only Kd. This is equivalent to locating the peaks of the function from the projections of the integrand onto the coordinate axes. The efficiency of VEGAS depends on the validity of this assumption. It is most efficient when the peaks of the integrand are well-localized. If an integrand can be rewritten in a form which is approximately separable this will increase the efficiency of integration with VEGAS.
so that the number of bins required is only Kd. This is equivalent to locating the peaks of the function from the projections of the integrand onto the coordinate axes. The efficiency of VEGAS depends on the validity of this assumption. It is most efficient when the peaks of the integrand are well-localized. If an integrand can be rewritten in a form which is approximately separable this will increase the efficiency of integration with VEGAS.
Variance reduction
In mathematics, more specifically in the theory of Monte Carlo methods, variance reduction is a procedure used to increase the precision of the estimates that can be obtained for a given number of iterations. Every output random variable from the simulation is associated with a variance which...
in Monte Carlo simulations by using a known or approximate probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
function to concentrate the search in those areas of the graph that make the greatest contribution to the final integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
.
The VEGAS algorithm is based on importance sampling
Importance sampling
In statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling in computational physics...
. It samples points from the probability distribution described by the function |f|, so that the points are concentrated in the regions that make the largest contribution to the integral.
In general, if the Monte Carlo integral of f is sampled with points distributed according to a probability distribution described by the function g, we obtain an estimate
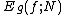 ,
,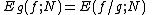
where
 is the Monte Carlo estimate of the integral of f,
is the Monte Carlo estimate of the integral of f,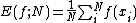
for N randomly distributed points
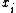 .
.The variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the new estimate is then
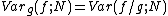
where
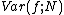 is the variance of the original estimate,
is the variance of the original estimate, 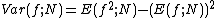 .
.If the probability distribution is chosen as
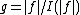 then it can be shown that the variance
then it can be shown that the variance 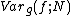 vanishes, and the error in the estimate will be zero. In practice it is not possible to sample from the exact distribution g for an arbitrary function, so importance sampling algorithms aim to produce efficient approximations to the desired distribution.
vanishes, and the error in the estimate will be zero. In practice it is not possible to sample from the exact distribution g for an arbitrary function, so importance sampling algorithms aim to produce efficient approximations to the desired distribution.The VEGAS algorithm approximates the exact distribution by making a number of passes over the integration region while histogramming the function f. Each histogram is used to define a sampling distribution for the next pass. Asymptotically this procedure converges to the desired distribution. In order to avoid the number of histogram bins growing like
 the probability distribution is approximated by a separable function:
the probability distribution is approximated by a separable function: 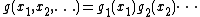 so that the number of bins required is only Kd. This is equivalent to locating the peaks of the function from the projections of the integrand onto the coordinate axes. The efficiency of VEGAS depends on the validity of this assumption. It is most efficient when the peaks of the integrand are well-localized. If an integrand can be rewritten in a form which is approximately separable this will increase the efficiency of integration with VEGAS.
so that the number of bins required is only Kd. This is equivalent to locating the peaks of the function from the projections of the integrand onto the coordinate axes. The efficiency of VEGAS depends on the validity of this assumption. It is most efficient when the peaks of the integrand are well-localized. If an integrand can be rewritten in a form which is approximately separable this will increase the efficiency of integration with VEGAS.

