
Unrestricted grammar
Encyclopedia
In formal language
theory, an unrestricted grammar is a formal grammar
on which no restrictions are made on the left and right sides of the grammar's productions. This is the most general class of grammars in the Chomsky–Schützenberger hierarchy, and can generate arbitrary recursively enumerable language
s.
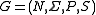 , where
, where 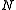 is a set of nonterminal symbols,
is a set of nonterminal symbols, 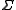 is a set of terminal symbols,
is a set of terminal symbols, 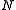 and
and 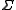 are disjoint (actually, this is not strictly necessary, because unrestricted grammars make no real distinction between nonterminal and terminal symbols, the designation exists purely so that one knows when to stop when trying to generate sentential forms of the grammar),
are disjoint (actually, this is not strictly necessary, because unrestricted grammars make no real distinction between nonterminal and terminal symbols, the designation exists purely so that one knows when to stop when trying to generate sentential forms of the grammar), 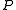 is a set of production rules of the form
is a set of production rules of the form 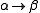 where
where  and
and 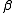 are strings of symbols in
are strings of symbols in 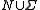 and
and  is not the empty string, and
is not the empty string, and 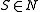 is a specially designated start symbol. As the name implies, there are no real restrictions on the types of production rules that unrestricted grammars can have.
is a specially designated start symbol. As the name implies, there are no real restrictions on the types of production rules that unrestricted grammars can have.
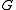 there exists some Turing machine
there exists some Turing machine
capable of recognizing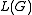 and vice-versa. Given an unrestricted grammar, such a Turing machine is simple enough to construct, as a two-tape nondeterministic Turing machine. The first tape contains the input word
and vice-versa. Given an unrestricted grammar, such a Turing machine is simple enough to construct, as a two-tape nondeterministic Turing machine. The first tape contains the input word 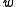 to be tested, and the second tape is used by the machine to generate sentential forms from
to be tested, and the second tape is used by the machine to generate sentential forms from 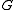 . The Turing machine then does the following:
. The Turing machine then does the following:
It is easy to see that this Turing machine will generate all and only the sentential forms of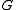 on its second tape after the last step is executed an arbitrary number of times, thus the language
on its second tape after the last step is executed an arbitrary number of times, thus the language 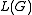 must be recursively enumerable.
must be recursively enumerable.
The reverse construction is also possible. Given some Turing machine, it is possible to create an unrestricted grammar.
of whether a given string belongs to the language of some unrestricted grammar is in general undecidable.
belongs to the language of some unrestricted grammar is in general undecidable.
It is perfectly possible to create a universal unrestricted grammar capable of accepting any other unrestricted grammar's language given a description of the language, just as it is possible to create a universal Turing machine
, so it would in theory be possible to build a programming language
based on unrestricted grammars (e.g. Thue
).
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory, an unrestricted grammar is a formal grammar
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
on which no restrictions are made on the left and right sides of the grammar's productions. This is the most general class of grammars in the Chomsky–Schützenberger hierarchy, and can generate arbitrary recursively enumerable language
Recursively enumerable language
In mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy of formal languages...
s.
Formal definition
An unrestricted grammar is a formal grammarFormal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
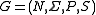 , where
, where 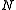 is a set of nonterminal symbols,
is a set of nonterminal symbols, 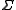 is a set of terminal symbols,
is a set of terminal symbols, 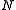 and
and 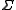 are disjoint (actually, this is not strictly necessary, because unrestricted grammars make no real distinction between nonterminal and terminal symbols, the designation exists purely so that one knows when to stop when trying to generate sentential forms of the grammar),
are disjoint (actually, this is not strictly necessary, because unrestricted grammars make no real distinction between nonterminal and terminal symbols, the designation exists purely so that one knows when to stop when trying to generate sentential forms of the grammar), 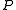 is a set of production rules of the form
is a set of production rules of the form 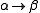 where
where  and
and 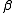 are strings of symbols in
are strings of symbols in 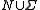 and
and  is not the empty string, and
is not the empty string, and 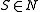 is a specially designated start symbol. As the name implies, there are no real restrictions on the types of production rules that unrestricted grammars can have.
is a specially designated start symbol. As the name implies, there are no real restrictions on the types of production rules that unrestricted grammars can have.Unrestricted grammars and Turing machines
It may be shown that unrestricted grammars characterize the recursively enumerable languages. This is the same as saying that for every unrestricted grammar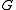 there exists some Turing machine
there exists some Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
capable of recognizing
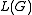 and vice-versa. Given an unrestricted grammar, such a Turing machine is simple enough to construct, as a two-tape nondeterministic Turing machine. The first tape contains the input word
and vice-versa. Given an unrestricted grammar, such a Turing machine is simple enough to construct, as a two-tape nondeterministic Turing machine. The first tape contains the input word 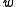 to be tested, and the second tape is used by the machine to generate sentential forms from
to be tested, and the second tape is used by the machine to generate sentential forms from 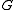 . The Turing machine then does the following:
. The Turing machine then does the following:- Start at the left of the second tape and repeatedly choose to move right or select the current position on the tape.
- NondeterministicallyNondeterminismNondeterminism may refer to:* Nondeterministic programming * Nondeterministic algorithm * Non-deterministic Turing machine * Indeterminacy in computation * Indeterminism...
choose a production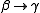 from the productions in
from the productions in 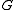 .
. - If
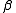 appears at some position on the second tape, replace
appears at some position on the second tape, replace 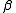 by
by 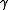 at that point, possibly shifting the symbols on the tape left or right depending on the relative lengths of
at that point, possibly shifting the symbols on the tape left or right depending on the relative lengths of 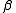 and
and 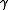 (e.g. if
(e.g. if 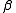 is longer than
is longer than 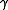 , shift the tape symbols left).
, shift the tape symbols left). - Compare the resulting sentential form on tape 2 to the word on tape 1. If they match, then the Turing machine accepts the word. If they don't go back to step 1.
It is easy to see that this Turing machine will generate all and only the sentential forms of
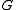 on its second tape after the last step is executed an arbitrary number of times, thus the language
on its second tape after the last step is executed an arbitrary number of times, thus the language 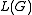 must be recursively enumerable.
must be recursively enumerable.The reverse construction is also possible. Given some Turing machine, it is possible to create an unrestricted grammar.
Computational properties
As might be expected from the equivalence of unrestricted grammars and Turing machines, the decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
of whether a given string
 belongs to the language of some unrestricted grammar is in general undecidable.
belongs to the language of some unrestricted grammar is in general undecidable.It is perfectly possible to create a universal unrestricted grammar capable of accepting any other unrestricted grammar's language given a description of the language, just as it is possible to create a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
, so it would in theory be possible to build a programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
based on unrestricted grammars (e.g. Thue
Thue (programming language)
Thue is an esoteric programming language invented by John Colagioia in early 2000. It is a meta-language that can be used to define or recognize Type-0 languages from the Chomsky hierarchy. Because it is able to define languages of such complexity, it is also Turing-complete itself...
).

