In geometric graph theory

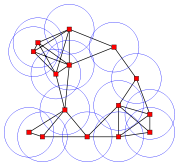
Geometric graph theory

In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...

, a unit disk graph is the intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

 of a family of unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

s in the Euclidean plane. That is, we form a vertex for each circle, and connect two vertices by an edge whenever the corresponding circles cross each other.

Characterizations

There are several possible definitions of the unit disk graph, equivalent to each other up to a choice of scale factor:

• An intersection graph of equal-radius circles, or of equal-radius disks
• A graph formed from a collection of equal-radius circles, in which two circles are connected by an edge if one circle contains the center of the other circle
• A graph formed from a collection of points in the Euclidean plane, in which two points are connected if their distance is below a fixed threshold

Properties

Every induced subgraph of a unit disk graph is also a unit disk graph. An example of a graph that is not a unit disk graph is the star

Star (graph theory)

In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...

 K_1,7 with one central node connected to seven leaves: if each of seven unit disks touches a common unit disk, some two of the seven disks must touch each other. Therefore, unit disk graphs cannot contain an induced K_1,7 subgraph.

Applications

Beginning with the work of , unit disk graphs have been used in computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

 to model the topology of ad-hoc wireless communication networks. In this application, nodes are connected through a direct wireless connection without a base station

Base station

The term base station can be used in the context of land surveying and wireless communications.- Land surveying :In the context of external land surveying, a base station is a GPS receiver at an accurately-known fixed location which is used to derive correction information for nearby portable GPS...

. It is assumed that all nodes are homogeneous and equipped with omnidirectional antenna

Omnidirectional antenna

In radio communication, an omnidirectional antenna is an antenna which radiates radio wave power uniformly in all directions in one plane, with the radiated power decreasing with elevation angle above or below the plane, dropping to zero on the antenna's axis. This radiation pattern is often...

s. Node locations are modeled as Euclidean points, and the area within which a signal from one node can be received by another node is modeled as a circle. If all nodes have transmitters of equal power, these circles are all equal. Random geometric graphs, formed as unit disk graphs with randomly generated disk centers, have also been used as a model of percolation and various other phenomena.

Computational complexity

It is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

 (more specifically, complete for the existential theory of the reals

Existential theory of the reals

In mathematical logic, computational complexity theory, and computer science, the existential theory of the reals is the set of all true sentences of the form...

) to determine whether a graph, given without geometry, can be represented as a unit disk graph. Additionally, it is provably impossible in polynomial time to output explicit coordinates of a unit disk graph representation: there exist unit disk graphs that require exponentially many bits of precision in any such representation.

However, many important and difficult graph optimization problems such as maximum independent set, graph coloring

Graph coloring

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...

, and minimum dominating set

Dominating set

In graph theory, a dominating set for a graph G =  is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...

 can be approximated

Approximation algorithm

In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...

 efficiently by using the geometric structure of these graphs, and the maximum clique problem can be solved exactly for these graphs in polynomial time, given a disk representation. More strongly, if a graph is given as input, it is possible in polynomial time to produce either a maximum clique or a proof that the graph is not a unit disk graph.

When a given vertex set forms a subset of a triangular lattice

Hexagonal lattice

The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...

, a necessary and sufficient condition for the perfectness

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

 of a unit graph is known. For the perfect graphs, a number of NP-complete optimization problems (graph coloring problem, maximum clique problem, and maximum independent set problem) are polynomially solvable.

See also

• Vietoris–Rips complex
  Vietoris–Rips complex
  In topology, the Vietoris–Rips complex, also called the Vietoris complex or Rips complex, is an abstract simplicial complex that can be defined from any metric space M and distance δ by forming a simplex for every finite set of points that has diameter at most δ...
  
  , a generalization of the unit disk graph that constructs higher-order topological spaces from unit distances in a metric space
• Unit distance graph
  Unit distance graph
  In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
  
  , a graph formed by connecting points that are at distance exactly one rather than (as here) at most a given threshold