
Unique games conjecture
Encyclopedia
In computational complexity theory
, the Unique Games Conjecture is a conjecture made by Subhash Khot
in 2002. The conjecture postulates that the problem of determining the value of a certain type of game, known as a unique game, has NP-hard
algorithmic complexity. It has applications in the theory of hardness of approximation
.
. The conjecture postulates the NP-hardness
of the following promise problem known as label cover with unique constraints. For each edge, the colors on the two vertices are restricted to some particular ordered pairs. In particular, unique constraints means that for each edge none of the ordered pairs have the same color for the same node.
This means that an instance of label cover with unique constraints over an alphabet of size k can be represented as a graph
together with a collection of permutation
s πe: [k] → [k], one for each edge e of the graph. An assignment to a label cover instance gives to each vertex of G a value in the set [k], often called “colours.”
Such instances are strongly constrained in the sense that the colour of a vertex uniquely defines the colours of its neighbours, and hence for its entire connected component. Thus, if the input instance admits a valid assignment, then such an assignment can be found efficiently by iterating over all colours of a single node. In particular, the problem of deciding if a given instance admits a satisfying assignment can be solved in polynomial time.
The value of a unique label cover instance is the fraction of constraints that can be satisfied by any assignment. For satisfiable instances, this value is 1 and is easy to find. On the other hand, it seems to be very difficult to determine the value of an unsatisfiable game, even approximatively. The unique games conjecture formalises this difficulty.
More formally, the (c, s) gap label cover problem with unique constraints is the following promise problem (Lyes, Lno):
where G is an instance of the label cover problem with unique constraints.
The unique games conjecture states that for every sufficiently small pair of constants ε, δ > 0, there exists a constant k such that the (1 - δ, ε) gap label cover problem with unique constraints over alphabet of size k is NP-hard
.
Instead of graphs, the label cover problem can be formulated in terms of linear equations. For example, suppose that we have a system of linear equations over the integers modulo 7:
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the Unique Games Conjecture is a conjecture made by Subhash Khot
Subhash Khot
Subhash Khot is an Associate Professor at New York University. He is best known for his Unique games conjecture.Khot obtained his bachelor’s degree in Computer Science from the Indian Institute of Technology Bombay in 1999. He received his doctorate degree in computer science from Princeton...
in 2002. The conjecture postulates that the problem of determining the value of a certain type of game, known as a unique game, has NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
algorithmic complexity. It has applications in the theory of hardness of approximation
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
.
Unique label cover
The following formulation of the unique games conjecture is often used in hardness of approximationHardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
. The conjecture postulates the NP-hardness
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
of the following promise problem known as label cover with unique constraints. For each edge, the colors on the two vertices are restricted to some particular ordered pairs. In particular, unique constraints means that for each edge none of the ordered pairs have the same color for the same node.
This means that an instance of label cover with unique constraints over an alphabet of size k can be represented as a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
together with a collection of permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s πe: [k] → [k], one for each edge e of the graph. An assignment to a label cover instance gives to each vertex of G a value in the set [k], often called “colours.”
Such instances are strongly constrained in the sense that the colour of a vertex uniquely defines the colours of its neighbours, and hence for its entire connected component. Thus, if the input instance admits a valid assignment, then such an assignment can be found efficiently by iterating over all colours of a single node. In particular, the problem of deciding if a given instance admits a satisfying assignment can be solved in polynomial time.
The value of a unique label cover instance is the fraction of constraints that can be satisfied by any assignment. For satisfiable instances, this value is 1 and is easy to find. On the other hand, it seems to be very difficult to determine the value of an unsatisfiable game, even approximatively. The unique games conjecture formalises this difficulty.
More formally, the (c, s) gap label cover problem with unique constraints is the following promise problem (Lyes, Lno):
- Lyes = {G: Some assignment satisfies at least a c-fraction of constraints in G}
- Lno = {G: Every assignment satisfies at most an s-fraction of constraints in G}
where G is an instance of the label cover problem with unique constraints.
The unique games conjecture states that for every sufficiently small pair of constants ε, δ > 0, there exists a constant k such that the (1 - δ, ε) gap label cover problem with unique constraints over alphabet of size k is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Instead of graphs, the label cover problem can be formulated in terms of linear equations. For example, suppose that we have a system of linear equations over the integers modulo 7:
-
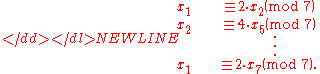
This is an instance of the label cover problem with unique constraints. For example, the first equation corresponds to the permutation π(1, 2) where π(1, 2)(x1) = 2x2 modulo 7.
Two-prover proof systems
A unique game is a special case of a two-prover one-round (2P1R) game. A two-prover one-round game has two players (also known as provers) and a referee. The referee sends each player a question drawn from a known probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, and the players each have to send an answer. The answers come from a set of fixed size. The game is specified by a predicate that depends on the questions sent to the players and the answers provided by them.
The players may decide on a strategy beforehand, although they cannot communicate with each other during the game. The players win if the predicate is satisfied by their questions and their answers.
A two-prover one-round game is called a unique game if for every pair of questions and every answer to the first question, there is exactly one answer to the second question that results in a win for the players, and vice versa. The value of a game is the maximum winning probability for the players over all strategies.
The unique games conjecture states that for every sufficiently small pair of constants ε, δ > 0, there exists a constant k such that the following promise problem (Lyes, Lno) is NP-hardNP-hardNP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
:- Lyes = {G: the value of G is at least 1 − δ}
- Lno = {G: the value of G is at most ε}
where G is a unique game whose answers come from a set of size k.
Probabilistically checkable proofs
Alternatively, the unique games conjecture postulates the existence of a certain type of probabilistically checkable proof for problems in NPNP (complexity)In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
.
A unique game can be viewed as a special kind of nonadaptive probabilistically checkable proof with query complexity 2, where for each pair of possible queries of the verifier and each possible answer to the first query, there is exactly one possible answer to the second query that makes the verifier accept, and vice versa.
The unique games conjecture states that for every sufficiently small pair of constants ε, δ > 0 there is a constant K such that every problem in NPNP (complexity)In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
has a probabilistically checkable proof over an alphabet of size K with completeness 1 - δ, soundness ε and randomness complexity O(log(n)) which is a unique game.
Relevance
Approximation results assuming P ≠ NP versus UGC Problem Poly-time approx. NP Hardness UGC Hardness Max 2-Sat 2-satisfiabilityIn computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
0.940... 0.954...+ε 0.940...+ε Max Cut Maximum cutFor a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the max-cut problem.The problem can be stated simply as follows...
0.878... 0.941...+ε 0.878...+ε Min Vertex Cover Vertex coverIn the mathematical discipline of graph theory, a vertex cover of a graph is a set of vertices such that each edge of the graph is incident to at least one vertex of the set....
2 1.360...-ε 2-ε
The unique games conjecture was introduced by Subhash Khot in 2002 in order to make progress on certain questions in the theory of hardness of approximationHardness of approximationIn computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
.
The truth of the unique games conjecture would imply the optimality of many known approximation algorithms (assuming P ≠ NP). For example, the approximation ratio achieved by the algorithm of Goemans and Williamson for approximating the maximum cutMaximum cutFor a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the max-cut problem.The problem can be stated simply as follows...
in a graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is optimal to within any additive constant assuming the unique games conjecture and P ≠ NP.
A list of results that the unique games conjecture is known to imply is shown in the table to the right together with the corresponding best results for the weaker assumption P≠NP. A constant of c+ε or c-ε means that the result holds for every constant (with respect to the problem size) strictly greater than or less than c, respectively.
Discussion and alternatives
Currently there is no consensus regarding the truth of the unique games conjecture. Certain stronger forms of the conjecture have been disproved.
A different form of the conjecture postulates that distinguishing the case when the value of a unique game is at least 1 − δ from the case when the value is at most ε is impossible for polynomial-time algorithms (but perhaps not NP-hard). This form of the conjecture would still be useful for applications in hardness of approximation.
The constant δ > 0 in the above formulations of the conjecture is necessary unless P = NP. If the uniqueness requirement is removed the corresponding statement is known to be true by the parallel repetition theorem, even when δ = 0.

