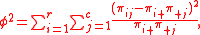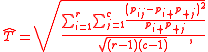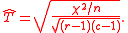Tschuprow's T

In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, Tschuprow's T is a measure of association

Association (statistics)

In statistics, an association is any relationship between two measured quantities that renders them statistically dependent. The term "association" refers broadly to any such relationship, whereas the narrower term "correlation" refers to a linear relationship between two quantities.There are many...

 between two nominal variables, giving a value between 0 and 1 (inclusive). It is closely related to Cramér's V

Cramér's V

In statistics, Cramér's V is a popular measure of association between two nominal variables, giving a value between 0 and +1...

, coinciding with it for square contingency tables.
It was published by Alexander Tschuprow

Alexander Alexandrovich Chuprov

Alexander Alexandrovich Chuprov Russian statistician who worked on mathematical statistics, sample survey theory and demography....

 (alternative spelling: Chuprov) in 1939.

Definition

For an r × c contingency table with r rows and c columns, let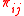 be the proportion of the population in cell 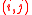and let 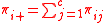and

Then the mean square contingency is given as

and Tschuprow's T as

Properties

T equals zero if and only if independence holds in the table, i.e., if and only if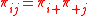 . T equals one if and only there is perfect dependence in the table, i.e., if and only if for each i there is only one j such that and vice versa. Hence, it can only equal 1 for square tables. In this it differs from Cramér's V

Cramér's V

In statistics, Cramér's V is a popular measure of association between two nominal variables, giving a value between 0 and +1...

, which can be equal to 1 for any rectangular table.

Estimation

If we have a multinomial sample of size n, the usual way to estimate T from the data is via the formula

where is the proportion of the sample in cell . This is the empirical value of T. With 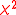the Pearson chi-square statistic

Pearson's chi-squared test

Pearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...

, this formula can also be written as

See also

Other measures of correlation for nominal data:

• Cramér's V
  Cramér's V
  In statistics, Cramér's V is a popular measure of association between two nominal variables, giving a value between 0 and +1...
  
  
• Phi coefficient
  Phi coefficient
  In statistics, the phi coefficient is a measure of association for two binary variables introduced by Karl Pearson. This measure is similar to the Pearson correlation coefficient in its interpretation...
  
  
• Uncertainty coefficient
  Uncertainty coefficient
  In statistics, the uncertainty coefficient, also called entropy coefficient or Theil's U, is a measure of nominal association. It was first introduced by Henri Theil and is based on the concept of information entropy. Suppose we have samples of two random variables, i and j...
  
  
• Lambda coefficient

Other related articles:

• Effect size
  Effect size
  In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...