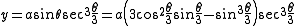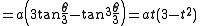Tschirnhausen cubic
Encyclopedia
In geometry
, Tschirnhausen cubic, is a plane curve
defined by the polar equation
, de L'Hôpital
and Catalan
. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.
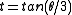. Then applying triple-angle formulas
gives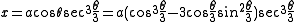
giving a parametric
form for the curve. The parameter t can be eliminated easily giving the Cartesian equation
.
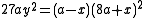If the curve is translated horizontally by 8a then the equations become
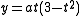
or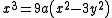
.
This gives an alternate polar form of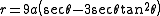
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Tschirnhausen cubic, is a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
defined by the polar equation
History
The curve was studied by von TschirnhausEhrenfried Walther von Tschirnhaus
Ehrenfried Walther von Tschirnhaus was a German mathematician, physicist, physician, and philosopher...
, de L'Hôpital
Guillaume de l'Hôpital
Guillaume François Antoine, Marquis de l'Hôpital was a French mathematician. His name is firmly associated with l'Hôpital's rule for calculating limits involving indeterminate forms 0/0 and ∞/∞...
and Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
. It was given the name Tschirnhausen cubic in a 1900 paper by R C Archibald, though it is sometimes known as de L'Hôpital's cubic or the trisectrix of Catalan.
Other equations
Put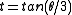. Then applying triple-angle formulasDe Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
gives
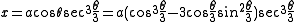
giving a parametric
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
form for the curve. The parameter t can be eliminated easily giving the Cartesian equation
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
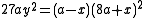.If the curve is translated horizontally by 8a then the equations become
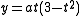
or
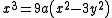.This gives an alternate polar form of
.
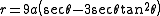