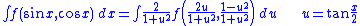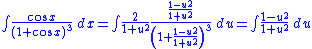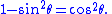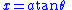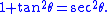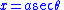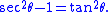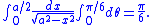In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, trigonometric substitution is the substitution of trigonometric functions for other expressions. One may use the trigonometric identities to simplify certain integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

s containing radical expressions:

• If the integrand contains a² − x², let

and use the identity

• If the integrand contains a² + x², let

and use the identity

• If the integrand contains x² − a², let

and use the identity

Integrals containing a² − x²

In the integral


we may use



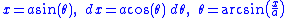
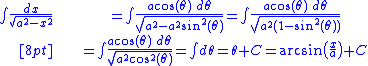
Note that the above step requires that a > 0 and cos(θ) > 0; we can choose the a to be the positive square root of a²; and we impose the restriction on θ to be −π/2 < θ < π/2 by using the arcsin function.

For a definite integral, one must figure out how the bounds of integration change. For example, as x goes from 0 to a/2, then sin(θ) goes from 0 to 1/2, so θ goes from 0 to π/6. Then we have

Some care is needed when picking the bounds. The integration above requires that −π/2 < θ < π/2, so θ going from 0 to π/6 is the only choice. If we had missed this restriction, we might have picked θ to go from π to 5π/6, which would result in the negative of the result.

Integrals containing a² + x²

In the integral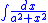


we may write



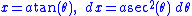
so that the integral becomes


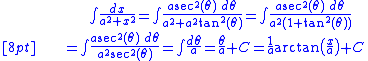
(provided a ≠ 0).

Integrals containing x² − a²

Integrals like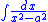


should be done by partial fractions

Partial fractions in integration

In integral calculus, partial fraction expansions provide an approach to integrating a general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of algebraic fractions...

 rather than trigonometric substitutions. However, the integral


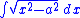
can be done by substitution:




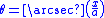
We can then solve this using the formula for the integral of secant cubed.

Substitutions that eliminate trigonometric functions

Substitution can be used to remove trigonometric functions. In particular, see Weierstrass substitution

Weierstrass substitution

In integral calculus, the Weierstrass substitution, named after Karl Weierstrass, is used for finding antiderivatives, and hence definite integrals, of rational functions of trigonometric functions. No generality is lost by taking these to be rational functions of the sine and cosine. The...

.

For instance,


(but be careful with the signs)