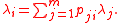Traffic equations
Encyclopedia
In queueing theory
, a discipline within the mathematical theory of probability
, traffic equations are equations that describe the mean arrival rate of traffic, allowing the arrival rates at individual nodes to be determined. Mitrani notes "if the network is stable, the traffic equations are valid and can be solved."
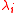at each node i in the network is given by the sum of external and internal arrivals. If external arrivals have rate 
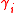and the routing matrix is P, the traffic equations are, (for i = 1, 2, ..., m)
This can be written in matrix form as
and there is a unique solution of unknowns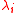
to this equation, so the mean arrival rates at each of the nodes can be determined given knowledge of the external arrival rates 
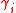and the matrix P. The matrix I − P is surely non-singular as otherwise in the long run the network would become empty.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a discipline within the mathematical theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, traffic equations are equations that describe the mean arrival rate of traffic, allowing the arrival rates at individual nodes to be determined. Mitrani notes "if the network is stable, the traffic equations are valid and can be solved."
Jackson network
In a Jackson network, the mean arrival rate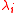 at each node i in the network is given by the sum of external and internal arrivals. If external arrivals have rate 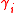and the routing matrix is P, the traffic equations are, (for i = 1, 2, ..., m)
This can be written in matrix form as
and there is a unique solution of unknowns
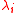to this equation, so the mean arrival rates at each of the nodes can be determined given knowledge of the external arrival rates 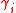and the matrix P. The matrix I − P is surely non-singular as otherwise in the long run the network would become empty.