
Taylor state
Encyclopedia
In plasma physics, a Taylor state is the minimum energy state of a plasma
satisfying the constraint of conserving magnetic helicity
.
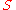 surrounding a plasma with negligible thermal energy (
surrounding a plasma with negligible thermal energy ( ).
).
Since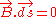 on
on 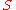 . This implies that
. This implies that 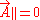 .
.
As discussed above, the plasma would relax towards a minimum energy state while conserving its magnetic helicity. Since the boundary is perfectly conducting, there cannot be any change in the associated flux. This implies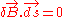 and
and 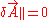 on
on 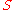 .
.
We formulate a variational problem of minimizing the plasma energy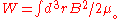 while conserving magnetic helicity
while conserving magnetic helicity 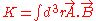 .
.
The variational problem is
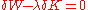 .
.
After some algebra this leads to the following constraint for the minimum energy state
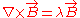 .
.
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
satisfying the constraint of conserving magnetic helicity
Magnetic helicity
In plasma physics, magnetic helicity is the extent to which a magnetic field "wraps around itself". It is a generalization of the topological concept of linking number to the differential quantities required to describe the magnetic field...
.
Derivation
Consider a closed, simply-connected, flux-conserving, perfectly conducting surface surrounding a plasma with negligible thermal energy (
surrounding a plasma with negligible thermal energy ( ).
).Since
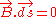 on
on 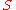 . This implies that
. This implies that 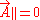 .
.As discussed above, the plasma would relax towards a minimum energy state while conserving its magnetic helicity. Since the boundary is perfectly conducting, there cannot be any change in the associated flux. This implies
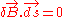 and
and 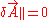 on
on 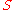 .
.We formulate a variational problem of minimizing the plasma energy
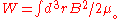 while conserving magnetic helicity
while conserving magnetic helicity 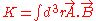 .
.The variational problem is
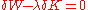 .
.After some algebra this leads to the following constraint for the minimum energy state
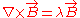 .
.

