
Taxicab number
Encyclopedia
In mathematics
, the nth taxicab number, typically denoted Ta(n) or Taxicab(n), is defined as the smallest number that can be expressed as a sum of two positive algebraic cubes in n distinct ways. The concept was first mentioned in 1657 by Bernard Frénicle de Bessy
, and was made famous in the early 20th century by a story involving Srinivasa Ramanujan
. In 1954, G. H. Hardy
and E. M. Wright
proved that such numbers exist for all positive integer
s n, and their proof is easily converted into a program to generate such numbers. However, the proof makes no claims at all about whether the thus-generated numbers are the smallest possible and thus it cannot be used to find the actual value of Ta(n).
The restriction of the summands to positive numbers is necessary, because allowing negative numbers allows for more (and smaller) instances of numbers that can be expressed as sums of cubes in n distinct ways. The concept of a cabtaxi number
has been introduced to allow for alternate, less restrictive definitions of this nature. In a sense, the specification of two summands and powers of three is also restrictive; the allows for these values to be other than two and three, respectively.
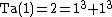
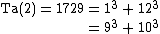

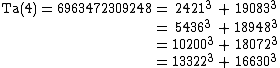
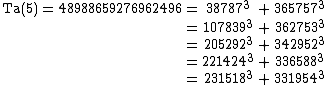
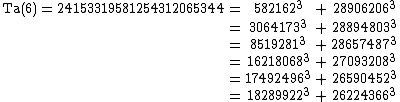
in 1657 and later immortalized by an incident involving mathematician
s G. H. Hardy
and Srinivasa Ramanujan
. As told by Hardy http://www-gap.dcs.st-and.ac.uk/~history/Quotations/Hardy.html:
The subsequent taxicab numbers were found with the help of computers. John Leech
obtained Ta(3) in 1957. E. Rosenstiel, J. A. Dardis and C. R. Rosenstiel found Ta(4) in 1991. J. A. Dardis found Ta(5) in 1994 and it was confirmed by David W. Wilson in 1999. Ta(6) was announced by Uwe Hollerbach on the NMBRTHRY mailing list on March 9, 2008, following a 2003 paper by Calude et al. that gave a 99% probability that the number was actually Ta(6). Upper bounds for Ta(7) to Ta(12) were found by Christian Boyer in 2006.
A more restrictive taxicab problem requires that the taxicab number be cubefree, which means that it is not divisible by any cube other than 13. When a cubefree taxicab number T is written as T = x3+y3, the numbers x and y must be relatively prime for all pairs (x, y). Among the taxicab numbers Ta(n) listed above, only Ta(1) and Ta(2) are cubefree taxicab numbers. The smallest cubefree taxicab number with three representations was discovered by Paul Vojta
(unpublished) in 1981 while he was a graduate student. It is
The smallest cubefree taxicab number with four representations was discovered by Stuart Gascoigne and independently by Duncan Moore in 2003. It is
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the nth taxicab number, typically denoted Ta(n) or Taxicab(n), is defined as the smallest number that can be expressed as a sum of two positive algebraic cubes in n distinct ways. The concept was first mentioned in 1657 by Bernard Frénicle de Bessy
Bernard Frénicle de Bessy
Bernard Frénicle de Bessy , was a French mathematician born in Paris, who wrote numerous mathematical papers, mainly in number theory and combinatorics. He is best remembered for Des quarrez ou tables magiques, a treatise on magic squares published posthumously in 1693, in which he described all...
, and was made famous in the early 20th century by a story involving Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
. In 1954, G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and E. M. Wright
E. M. Wright
Sir Edward Maitland Wright was an English mathematician.He is best known for co-authoring “Hardy and Wright”, An Introduction to the Theory of Numbers, with G. H...
proved that such numbers exist for all positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s n, and their proof is easily converted into a program to generate such numbers. However, the proof makes no claims at all about whether the thus-generated numbers are the smallest possible and thus it cannot be used to find the actual value of Ta(n).
The restriction of the summands to positive numbers is necessary, because allowing negative numbers allows for more (and smaller) instances of numbers that can be expressed as sums of cubes in n distinct ways. The concept of a cabtaxi number
Cabtaxi number
In mathematics, the n-th cabtaxi number, typically denoted Cabtaxi, is defined as the smallest positive integer that can be written as the sum of two positive or negative or 0 cubes in n ways...
has been introduced to allow for alternate, less restrictive definitions of this nature. In a sense, the specification of two summands and powers of three is also restrictive; the allows for these values to be other than two and three, respectively.
Known taxicab numbers
So far, the following six taxicab numbers are known :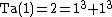
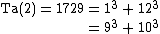

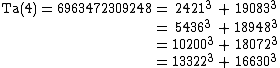
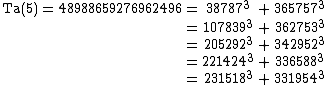
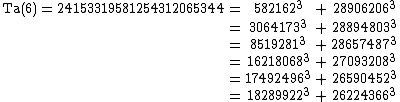
Discovery history
Ta(2), also known as the Hardy-Ramanujan number, was first published by Bernard Frénicle de BessyBernard Frénicle de Bessy
Bernard Frénicle de Bessy , was a French mathematician born in Paris, who wrote numerous mathematical papers, mainly in number theory and combinatorics. He is best remembered for Des quarrez ou tables magiques, a treatise on magic squares published posthumously in 1693, in which he described all...
in 1657 and later immortalized by an incident involving mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
. As told by Hardy http://www-gap.dcs.st-and.ac.uk/~history/Quotations/Hardy.html:
The subsequent taxicab numbers were found with the help of computers. John Leech
John Leech (mathematician)
John Leech was a British mathematician working in number theory, geometry and combinatorial group theory. He is best known for his discovery of the Leech lattice in 1965. He also discovered Ta in 1957...
obtained Ta(3) in 1957. E. Rosenstiel, J. A. Dardis and C. R. Rosenstiel found Ta(4) in 1991. J. A. Dardis found Ta(5) in 1994 and it was confirmed by David W. Wilson in 1999. Ta(6) was announced by Uwe Hollerbach on the NMBRTHRY mailing list on March 9, 2008, following a 2003 paper by Calude et al. that gave a 99% probability that the number was actually Ta(6). Upper bounds for Ta(7) to Ta(12) were found by Christian Boyer in 2006.
A more restrictive taxicab problem requires that the taxicab number be cubefree, which means that it is not divisible by any cube other than 13. When a cubefree taxicab number T is written as T = x3+y3, the numbers x and y must be relatively prime for all pairs (x, y). Among the taxicab numbers Ta(n) listed above, only Ta(1) and Ta(2) are cubefree taxicab numbers. The smallest cubefree taxicab number with three representations was discovered by Paul Vojta
Paul Vojta
Paul Alan Vojta is an American mathematician, known for his work in number theory on diophantine geometry and diophantine approximation....
(unpublished) in 1981 while he was a graduate student. It is
- 15170835645
- = 5173 + 24683
- = 7093 + 24563
- = 17333 + 21523.
The smallest cubefree taxicab number with four representations was discovered by Stuart Gascoigne and independently by Duncan Moore in 2003. It is
- 1801049058342701083
- = 922273 + 12165003
- = 1366353 + 12161023
- = 3419953 + 12076023
- = 6002593 + 11658843

