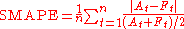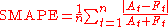Symmetric mean absolute percentage error
Encyclopedia
Symmetric mean absolute percentage error (SMAPE or sMAPE) is an accuracy measure based on percentage (or relative) errors. It is usually defined as follows:
where At is the actual value and Ft is the forecast value.
The absolute difference
between At and Ft is divided by half the sum of the actual value At and the forecast value Ft. The value of this calculation is summed for every fitted point t and divided again by the number of fitted points n. The earliest reference to this formula appears to be Armstrong (1985, p. 348) where it is called "adjusted MAPE
". It has been later discussed, modified and re-proposed by Flores (1986).
In contrast to the mean absolute percentage error
, SMAPE has a both lower bound and an upper bound. Indeed, the formula above provides a result between 0% and 200%. However a percentage error between 0% and 100% is much easier to interpret. That is the reason why the formula below is often used in practice (i.e. no factor 0.5 in denominator):
However, one problem with SMAPE is that it is not as symmetric as it sounds since over- and under-forecasts are not treated equally. Let's consider the following example by applying the second SMAPE formula:
where At is the actual value and Ft is the forecast value.
The absolute difference
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
between At and Ft is divided by half the sum of the actual value At and the forecast value Ft. The value of this calculation is summed for every fitted point t and divided again by the number of fitted points n. The earliest reference to this formula appears to be Armstrong (1985, p. 348) where it is called "adjusted MAPE
Mape
-Things:* Mape, a toe loop jump in figure skating, after Bruce Mapes* Mape, a novel by André Maurois* MAPE, mean absolute percentage error-Places:* Mape , a town in Cova Lima District, East Timor* Lake Mape a lake and national park in Sierra Leone...
". It has been later discussed, modified and re-proposed by Flores (1986).
In contrast to the mean absolute percentage error
Mean Absolute Percentage Error
Mean absolute percentage error is measure of accuracy in a fitted time series value in statistics, specifically trending. It usually expresses accuracy as a percentage, and is defined by the formula:...
, SMAPE has a both lower bound and an upper bound. Indeed, the formula above provides a result between 0% and 200%. However a percentage error between 0% and 100% is much easier to interpret. That is the reason why the formula below is often used in practice (i.e. no factor 0.5 in denominator):
However, one problem with SMAPE is that it is not as symmetric as it sounds since over- and under-forecasts are not treated equally. Let's consider the following example by applying the second SMAPE formula:
- Over-forecasting: At = 100 and Ft = 110 give SMAPE = 4.76%
- Under-forecasting: At = 100 and Ft = 90 give SMAPE = 5.26%.
See also
- Relative change and differenceRelative change and differenceThe relative difference, percent difference, relative percent difference, or percentage difference between two quantities is the difference between them, expressed as a comparison to the size of one or both of them. Such measures are unitless numbers...
- Mean absolute errorMean absolute errorIn statistics, the mean absolute error is a quantity used to measure how close forecasts or predictions are to the eventual outcomes. The mean absolute error is given by...
- Mean absolute percentage errorMean Absolute Percentage ErrorMean absolute percentage error is measure of accuracy in a fitted time series value in statistics, specifically trending. It usually expresses accuracy as a percentage, and is defined by the formula:...
- Mean squared errorMean squared errorIn statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
- Root mean squared error