
Sylvester's determinant theorem
Encyclopedia
In matrix
theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinant
s. It is named after James Joseph Sylvester
.
The theorem states that if A, B are matrices of size p × n and n × p respectively, then
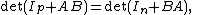
where Ia is the identity matrix
of order a.
It is closely related to the Matrix determinant lemma
and its generalization.
This theorem is useful in developing a Bayes estimator
for multivariate Gaussian distributions.
Sylvester (1857) stated this theorem without proof.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s. It is named after James Joseph Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
.
The theorem states that if A, B are matrices of size p × n and n × p respectively, then
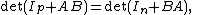
where Ia is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of order a.
It is closely related to the Matrix determinant lemma
Matrix determinant lemma
In mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertiblematrix Aand the dyadic product, u vT,of a column vector u and a row vector vT.- Statement :...
and its generalization.
This theorem is useful in developing a Bayes estimator
Bayes estimator
In estimation theory and decision theory, a Bayes estimator or a Bayes action is an estimator or decision rule that minimizes the posterior expected value of a loss function . Equivalently, it maximizes the posterior expectation of a utility function...
for multivariate Gaussian distributions.
Sylvester (1857) stated this theorem without proof.

