Matrix determinant lemma
Encyclopedia
In mathematics
, in particular linear algebra
, the matrix determinant lemma computes the determinant
of the sum of an invertible
matrix
A
and the dyadic product, u vT,
of a column vector u and a row vector vT.
the matrix determinant lemma states that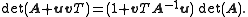
Here, uvT is the dyadic product of two vectors u and v.
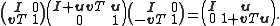
The determinant of the left hand side is the product of the determinants of the three matrices. Since the first and third matrix are triangle matrices with unit diagonal, their determinants are just 1. The determinant of the middle matrix is our desired value. The determinant of the right hand side is simply (1 + vTu). So we have the result:
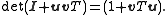
Then the general case can be found as: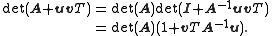
numerically cheap way
to compute the determinant of A corrected by the matrix uvT. The computation is relatively cheap because the determinant of A+uvT
does not have to be computed from scratch (which in general is expensive). Using unit vectors for u and/or v, individual columns, rows or elements of A may be manipulated and a correspondingly updated determinant computed relatively cheaply in this way.
When the matrix determinant lemma is used in conjunction with the Sherman-Morrison formula
, both the inverse and determinant may be conveniently updated together.
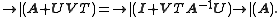
In the special case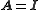
this is Sylvester's theorem for determinants
.
Given additionally an invertible m-by-m matrix W, the relationship can also be expressed as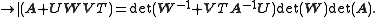
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the matrix determinant lemma computes the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the sum of an invertible
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A
and the dyadic product, u vT,
of a column vector u and a row vector vT.
Statement
Suppose A is an invertible square matrix and u, v are column vectors. Thenthe matrix determinant lemma states that
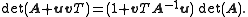
Here, uvT is the dyadic product of two vectors u and v.
Proof
First the proof of the special case A = I follows from the equality: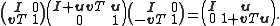The determinant of the left hand side is the product of the determinants of the three matrices. Since the first and third matrix are triangle matrices with unit diagonal, their determinants are just 1. The determinant of the middle matrix is our desired value. The determinant of the right hand side is simply (1 + vTu). So we have the result:
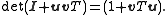
Then the general case can be found as:
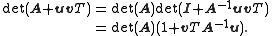
Application
If the determinant and inverse of A are already known, the formula provides anumerically cheap way
to compute the determinant of A corrected by the matrix uvT. The computation is relatively cheap because the determinant of A+uvT
does not have to be computed from scratch (which in general is expensive). Using unit vectors for u and/or v, individual columns, rows or elements of A may be manipulated and a correspondingly updated determinant computed relatively cheaply in this way.
When the matrix determinant lemma is used in conjunction with the Sherman-Morrison formula
Sherman-Morrison formula
In mathematics, in particular linear algebra, the Sherman–Morrison formula, named after Jack Sherman and Winifred J. Morrison, computes the inverse of the sum of an invertiblematrix Aand the dyadic product, u v^T,of a column vector u and a row vector v^T...
, both the inverse and determinant may be conveniently updated together.
Generalization
Suppose A is an invertible n-by-n matrix and U, V are n-by-m matrices. Then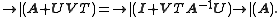In the special case
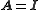this is Sylvester's theorem for determinantsSylvester's determinant theorem
In matrix theory, Sylvester's determinant theorem is a theorem useful for evaluating certain types of determinants. It is named after James Joseph Sylvester....
.
Given additionally an invertible m-by-m matrix W, the relationship can also be expressed as
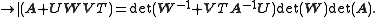
See also
- The Sherman-Morrison formulaSherman-Morrison formulaIn mathematics, in particular linear algebra, the Sherman–Morrison formula, named after Jack Sherman and Winifred J. Morrison, computes the inverse of the sum of an invertiblematrix Aand the dyadic product, u v^T,of a column vector u and a row vector v^T...
, which shows how to update the inverse, A−1, to obtain (A+uvT)−1. - The Woodbury formulaWoodbury matrix identityIn mathematics , the Woodbury matrix identity, named after Max A. Woodbury says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix...
, which shows how to update the inverse, A−1, to obtain (A+UCVT)−1.