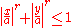In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a super-ellipsoid or superellipsoid is a solid whose horizontal sections are super-ellipses (Lamé curves) with the same exponent r, and whose vertical sections through the center are super-ellipses with the same exponent t.

Super-ellipsoids as computer graphics

Computer graphics

Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....

 primitives were popularized by Alan H. Barr (who used the name "superquadrics" to refer to both superellipsoids and supertoroid

Supertoroid

In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces whose shape is defined by mathematical formulas similar to those that define the superquadrics...

s). However, while some super-ellipsoids are superquadrics, neither family is contained in the other.

Piet Hein

Piet Hein

Piet Hein is the name of:* Piet Pieterszoon Hein , Dutch naval commander and folk hero* Piet Hein , descendant of the above, Danish poet and scientist...

's superegg

Superegg

In geometry, a superegg is a solid of revolution obtained by rotating an elongated super-ellipse with exponent greater than 2 around its longest axis. It is a special case of super-ellipsoid....

s are special cases of super-ellipsoids.

Basic shape

The basic super-ellipsoid is defined by the implicit equation

Implicit function

The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...

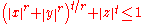
The parameters r and t are positive real numbers that control the amount of flattening at the tips and at the equator. Note that the formula becomes a special case of the superquadric's equation if (and only if) t = r.

Any "parallel of latitude" of the superellipsoid (a horizontal section at any constant z between -1 and +1) is a Lamé curve with exponent r, scaled by :

Any "meridian of longitude" (a section by any vertical plane through the origin) is a Lamé curve with exponent t, stretched horizontally by a factor w that depends on the sectioning plane. Namely, if x = u cos θ and y = u sin θ, for a fixed θ, then

where


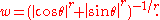
In particular, if r is 2, the horizontal cross-sections are circles, and the horizontal stretching w of the vertical sections is 1 for all planes. In that case, the super-ellipsoid is a solid of revolution

Solid of revolution

In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....

, obtained by rotating the Lamé curve with exponent t around the vertical axis.

The basic shape above extends from −1 to +1 along each coordinate axis. The general super-ellipsoid is obtained by scaling the basic shape along each axis by factors A, B, C, the semi-diameters of the resulting solid. The implicit equation is


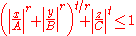
Setting r = 2, t = 2.5, A = B = 3, C = 4 one obtains Piet Hein's superegg.

The general superellipsoid has a parametric representation in terms of surface parameters u and v (longitude and latitude):


where the auxiliary functions are

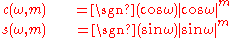
and the sign function

Sign function

In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....

 sgn(x) is

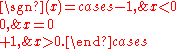
The volume inside this surface can be expressed in terms of beta functions, β(m,n) = Γ(m)Γ(n)/Γ(m + n), as

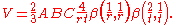
External links

• Bibliography: SuperQuadric Representations
• Superquadric Tensor Glyphs
• SuperQuadric Ellipsoids and Toroids, OpenGL Lighting, and Timing
• Superquadratics by Robert Kragler, The Wolfram Demonstrations Project.