Superdense coding
Encyclopedia
Superdense coding is a technique used in quantum information theory to send two bits of classical information using only one qubit, with the aid of entanglement
.
s, instead of classical bit
s. Alice would encode the classical information in a qubit and send it to Bob. After receiving the qubit, Bob recovers the classical information via measurement
. The question is: how much classical information can be transmitted per qubit? Since non-orthogonal quantum states cannot be distinguished reliably, one would guess that Alice can do no better than one classical bit per qubit. Indeed this bound
on efficiency has been proven formally. Thus there is no advantage gained in using qubits instead of classical bits. However, with the additional assumption that Alice and Bob share an entangled state, two classical bits per qubit can be achieved. The term superdense refers to this doubling of efficiency.
Suppose parts of a Bell state
, say
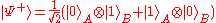
are distributed to Alice and Bob. The first subsystem, denoted by subscript A, belongs to Alice and the second, B, system to Bob. By only manipulating her particle locally, Alice can transform the composite system into any one of the Bell states (this is not entirely surprising, for entanglement cannot be broken using local operations):
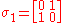
(notice this is one of the Pauli matrices
), the total two-particle system now is in state
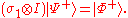
So, depending on the message she would like to send, Alice performs one of the four local operations given above and sends her qubit to Bob. By performing a projective measurement in the Bell basis on the two particle system, Bob decodes the desired message.
Notice, however, that if some mischievous person, Eve, intercepts Alice's qubit en route to Bob, all that is obtained by Eve is part of an entangled state. Therefore, no useful information whatsoever is gained by Eve unless she can interact with Bob's qubit.
s. Alice and Bob share a maximally entangled state ω. Let the subsystems initially possessed by Alice and Bob be labeled 1 and 2, respectively. To transmit the message x, Alice applies an appropriate channel
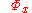
on subsystem 1. On the combined system, this is effected by
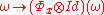
where Id denotes the identity map on subsystem 2. Alice then sends her subsystem to Bob, who performs a measurement on the combined system to recover the message. Let the effects of Bob's measurement be Fy. The probability that Bob's measuring apparatus registers the message y is
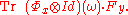
Therefore, to achieve the desired transmission, we require that
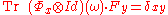
where δxy is the Kronecker delta.
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
.
Overview
Suppose Alice would like to send classical information to Bob using qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s, instead of classical bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s. Alice would encode the classical information in a qubit and send it to Bob. After receiving the qubit, Bob recovers the classical information via measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
. The question is: how much classical information can be transmitted per qubit? Since non-orthogonal quantum states cannot be distinguished reliably, one would guess that Alice can do no better than one classical bit per qubit. Indeed this bound
Holevo's theorem
In physics, in the area of quantum information theory, Holevo's theorem is an important limitative theorem in quantum computing which was published by in 1973....
on efficiency has been proven formally. Thus there is no advantage gained in using qubits instead of classical bits. However, with the additional assumption that Alice and Bob share an entangled state, two classical bits per qubit can be achieved. The term superdense refers to this doubling of efficiency.
Details
Crucial to this procedure is the shared entangled state between Alice and Bob, and the property of entangled states that a (maximally) entangled state can be transformed into another state via local manipulation.Suppose parts of a Bell state
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
, say
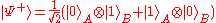
are distributed to Alice and Bob. The first subsystem, denoted by subscript A, belongs to Alice and the second, B, system to Bob. By only manipulating her particle locally, Alice can transform the composite system into any one of the Bell states (this is not entirely surprising, for entanglement cannot be broken using local operations):
- Obviously, if Alice does nothing, the system remains in the state
.
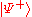- If Alice sends her particle through the unitary gate
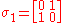
(notice this is one of the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
), the total two-particle system now is in state
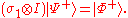
- If
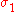is replaced by 
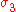, the initial state 
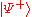is transformed into 
.
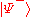- Similarly, if Alice applies
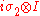to the system, the resultant state is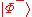 
So, depending on the message she would like to send, Alice performs one of the four local operations given above and sends her qubit to Bob. By performing a projective measurement in the Bell basis on the two particle system, Bob decodes the desired message.
Notice, however, that if some mischievous person, Eve, intercepts Alice's qubit en route to Bob, all that is obtained by Eve is part of an entangled state. Therefore, no useful information whatsoever is gained by Eve unless she can interact with Bob's qubit.
General dense coding scheme
General dense coding schemes can be formulated in the language used to describe quantum channelQuantum channel
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
s. Alice and Bob share a maximally entangled state ω. Let the subsystems initially possessed by Alice and Bob be labeled 1 and 2, respectively. To transmit the message x, Alice applies an appropriate channel
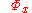
on subsystem 1. On the combined system, this is effected by
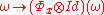
where Id denotes the identity map on subsystem 2. Alice then sends her subsystem to Bob, who performs a measurement on the combined system to recover the message. Let the effects of Bob's measurement be Fy. The probability that Bob's measuring apparatus registers the message y is
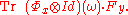
Therefore, to achieve the desired transmission, we require that
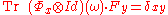
where δxy is the Kronecker delta.