Super-recursive algorithm
Encyclopedia
In computability theory
, super-recursive algorithms are a generalization of ordinary algorithm
s that are more powerful, that is, compute more than Turing machines. The term was introduced by Mark Burgin, whose book "Super-recursive algorithms" develops their theory and presents several mathematical models. Turing machines and other mathematical models of conventional algorithms allow researchers to find properties of recursive algorithms and their computations. In a similar way, mathematical models of super-recursive algorithms, such as inductive Turing machines, allow researchers to find properties of super-recursive algorithms and their computations.
Burgin, as well as other researchers (including Selim Akl
, Eugene Eberbach, Peter Kugel, Jan van Leeuwen
, Hava Siegelmann, Peter Wegner, and Jiří Wiedermann) who studied different kinds of super-recursive algorithms and contributed to the theory of super-recursive algorithms, have argued that super-recursive algorithms can be used to disprove the Church-Turing thesis, but this point of view has been criticized within the mathematical community and is not widely accepted.
s that can be implemented on Turing machines, and uses the word algorithm in a more general sense. Then a super-recursive class of algorithms is "a class of algorithms in which it is possible to compute functions not computable by any Turing machine
" (Burgin 2005: 107).
Super-recursive algorithms are closely related to hypercomputation
in a way similar to the relationship between ordinary computation and ordinary algorithms. Computation is a process, while an algorithm is a finite constructive description of such a process. Thus a super-recursive algorithm defines a "computational process (including processes of input and output) that cannot be realized by recursive algorithms." (Burgin 2005: 108). A more restricted definition demands that hypercomputation
solves a supertask
(see Copeland 2002; Hagar and Korolev 2007).
Super-recursive algorithms are also related to algorithmic schemes, which are more general than super-recursive algorithms. Burgin argues (2005: 115) that it is necessary to make a clear distinction between super-recursive algorithms and those algorithmic schemes that are not algorithms. Under this distinction, some types of hypercomputation are obtained by super-recursive algorithms, e.g., inductive Turing machines, while other types of hypercomputation are directed by algorithmic schemas, e.g., infinite time Turing machines. This explains how works on super-recursive algorithms are related to hypercomputation and vice versa. According to this argument, super-recursive algorithms are just one way of defining a hypercomputational process.
Examples of algorithmic schemes include:
For examples of practical super-recursive algorithms, see the book of Burgin.
is that an ordinary Turing machine must stop when it has obtained its result, while in some cases an inductive Turing machine can continue to compute after obtaining the result, without stopping. Kleene called procedures that could run forever without stopping by the name calculation procedure or algorithm (Kleene 1952:137). Kleene also demanded that such an algorithm must eventually exhibit "some object" (Kleene 1952:137). Burgin argues that this condition is satisfied by inductive Turing machines, as their results are exhibited after a finite number of steps. The reason that inductive Turing machines cannot be instructed to halt when their final output is produced is that in some cases inductive Turing machines may not be able to tell at which step the result has been obtained.
Simple inductive Turing machines are equivalent to other models of computation such as general Turing machines of Schmidhuber, trial and error predicates of Hilary Putnam, limiting partial recursive functions of Gold, and trial-and-error machines of Hintikka and Mutanen. More advanced inductive Turing machines are much more powerful. There are hierarchies of inductive Turing machines that can decide membership in arbitrary sets of the arithmetical hierarchy
(Burgin 2005). In comparison with other equivalent models of computation, simple inductive Turing machines and general Turing machines give direct constructions of computing automata that are thoroughly grounded in physical machines. In contrast, trial-and-error predicates, limiting recursive functions, and limiting partial recursive functions present only syntactic systems of symbols with formal rules for their manipulation. Simple inductive Turing machines and general Turing machines are related to limiting partial recursive functions and trial-and-error predicates as Turing machines are related to partial recursive functions and lambda calculus.
The non-halting computations of inductive Turing machines should not be confused with infinite-time computations (see, for example, Potgieter 2006). First, some computations of inductive Turing machines do halt. As in the case of conventional Turing machines, some halting computations give the result, while others do not. Even it does not halt, an inductive Turing machine produces output from time to time. If this output stops changing, it is then considered the result of the computation.
There are two main distinctions between ordinary Turing machines and simple inductive Turing machines. The first distinction is that even simple inductive Turing machines can do much more than conventional Turing machines. The second distinction is that a conventional Turing machine will always determine (by coming to a final state) when the result is obtained, while a simple inductive Turing machine, in some cases (such as when "computing" something that cannot be computed by an ordinary Turing machine), will not be able to make this determination.
that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π but still excludes most of the real numbers, because most cannot be described by a finite program. Traditional Turing machine
s cannot edit their previous outputs; generalized Turing machines, according to Jürgen Schmidhuber
, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges, that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt Gödel
(1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problem
could be solved. Schmidhuber (2000, 2002) uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everything
. Generalized Turing machines and simple inductive Turing machines are two classes of super-recursive algorithms that are the closest to recursive algorithms.
. He proves furthermore that super-recursive algorithms could theoretically provide even greater efficiency gains than using quantum algorithms.
Burgin's interpretation of super-recursive algorithms has encountered opposition in the mathematical community. One critic is logician Martin Davis
, who argues that Burgin's claims have been well understood "for decades". Davis states,
Davis disputes Burgin's claims that sets at level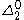
of the arithmetical hierarchy
can be called computable, saying
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, super-recursive algorithms are a generalization of ordinary algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s that are more powerful, that is, compute more than Turing machines. The term was introduced by Mark Burgin, whose book "Super-recursive algorithms" develops their theory and presents several mathematical models. Turing machines and other mathematical models of conventional algorithms allow researchers to find properties of recursive algorithms and their computations. In a similar way, mathematical models of super-recursive algorithms, such as inductive Turing machines, allow researchers to find properties of super-recursive algorithms and their computations.
Burgin, as well as other researchers (including Selim Akl
Selim Akl
Selim G. Akl is a professor at Queen's University in the Queen's School of Computing, where he leads the . His research interests are primarily in the area of algorithm design and analysis, in particular for problems in parallel computing and unconventional computing. He is married, and has three...
, Eugene Eberbach, Peter Kugel, Jan van Leeuwen
Jan van Leeuwen
Jan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
, Hava Siegelmann, Peter Wegner, and Jiří Wiedermann) who studied different kinds of super-recursive algorithms and contributed to the theory of super-recursive algorithms, have argued that super-recursive algorithms can be used to disprove the Church-Turing thesis, but this point of view has been criticized within the mathematical community and is not widely accepted.
Definition
Burgin (2005: 13) uses the term recursive algorithms for algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s that can be implemented on Turing machines, and uses the word algorithm in a more general sense. Then a super-recursive class of algorithms is "a class of algorithms in which it is possible to compute functions not computable by any Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
" (Burgin 2005: 107).
Super-recursive algorithms are closely related to hypercomputation
Hypercomputation
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms...
in a way similar to the relationship between ordinary computation and ordinary algorithms. Computation is a process, while an algorithm is a finite constructive description of such a process. Thus a super-recursive algorithm defines a "computational process (including processes of input and output) that cannot be realized by recursive algorithms." (Burgin 2005: 108). A more restricted definition demands that hypercomputation
Hypercomputation
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms...
solves a supertask
Supertask
In philosophy, a supertask is a quantifiably infinite number of operations that occur sequentially within a finite interval of time. Supertasks are called "hypertasks" when the number of operations becomes innumerably infinite. The term supertask was coined by the philosopher James F...
(see Copeland 2002; Hagar and Korolev 2007).
Super-recursive algorithms are also related to algorithmic schemes, which are more general than super-recursive algorithms. Burgin argues (2005: 115) that it is necessary to make a clear distinction between super-recursive algorithms and those algorithmic schemes that are not algorithms. Under this distinction, some types of hypercomputation are obtained by super-recursive algorithms, e.g., inductive Turing machines, while other types of hypercomputation are directed by algorithmic schemas, e.g., infinite time Turing machines. This explains how works on super-recursive algorithms are related to hypercomputation and vice versa. According to this argument, super-recursive algorithms are just one way of defining a hypercomputational process.
Examples
Examples of super-recursive algorithms include (Burgin 2005: 132):- limiting recursive functions and limiting partial recursive functions (E.M. Gold)
- trial and error predicates (Hilary Putnam)
- inductive inference machines (Carl Smith)
- inductive Turing machines, which perform computations similar to computations of Turing machines and produce their results after a finite number of steps (Mark Burgin)
- limit Turing machines, which perform computations similar to computations of Turing machines but their final results are limits of their intermediate results (Mark Burgin)
- trial-and-error machines (Ja. Hintikka and A. Mutanen)
- general Turing machines (J. Schmidhuber)
- Internet machines (van Leeuwen, J.Jan van LeeuwenJan van Leeuwen is a Dutch computer scientist, a professor at the Department of Information and Computing Sciences at the Utrecht University....
and Wiedermann, J.) - evolutionary computers, which use DNA to produce the value of a function (Darko Roglic)
- fuzzy computation (Jirí Wiedermann)
- evolutionary Turing machines (Eugene Eberbach)
Examples of algorithmic schemes include:
- Turing machines with arbitrary oracles (Alan Turing)
- Transrecursive operators (Borodyanskii and Burgin)
- machines that compute with real numbers (L. Blum, F. Cucker, M. Shub, and S. Smale)
- neural networks based on real numbers (Hava Siegelmann)
For examples of practical super-recursive algorithms, see the book of Burgin.
Inductive Turing machines
Inductive Turing machines implement an important class of super-recursive algorithms. An inductive Turing machine is a definite list of well-defined instructions for completing a task, when given an initial state, will proceed through a well-defined series of successive states, eventually giving the final result. The difference between an inductive Turing machine and an ordinary Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
is that an ordinary Turing machine must stop when it has obtained its result, while in some cases an inductive Turing machine can continue to compute after obtaining the result, without stopping. Kleene called procedures that could run forever without stopping by the name calculation procedure or algorithm (Kleene 1952:137). Kleene also demanded that such an algorithm must eventually exhibit "some object" (Kleene 1952:137). Burgin argues that this condition is satisfied by inductive Turing machines, as their results are exhibited after a finite number of steps. The reason that inductive Turing machines cannot be instructed to halt when their final output is produced is that in some cases inductive Turing machines may not be able to tell at which step the result has been obtained.
Simple inductive Turing machines are equivalent to other models of computation such as general Turing machines of Schmidhuber, trial and error predicates of Hilary Putnam, limiting partial recursive functions of Gold, and trial-and-error machines of Hintikka and Mutanen. More advanced inductive Turing machines are much more powerful. There are hierarchies of inductive Turing machines that can decide membership in arbitrary sets of the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
(Burgin 2005). In comparison with other equivalent models of computation, simple inductive Turing machines and general Turing machines give direct constructions of computing automata that are thoroughly grounded in physical machines. In contrast, trial-and-error predicates, limiting recursive functions, and limiting partial recursive functions present only syntactic systems of symbols with formal rules for their manipulation. Simple inductive Turing machines and general Turing machines are related to limiting partial recursive functions and trial-and-error predicates as Turing machines are related to partial recursive functions and lambda calculus.
The non-halting computations of inductive Turing machines should not be confused with infinite-time computations (see, for example, Potgieter 2006). First, some computations of inductive Turing machines do halt. As in the case of conventional Turing machines, some halting computations give the result, while others do not. Even it does not halt, an inductive Turing machine produces output from time to time. If this output stops changing, it is then considered the result of the computation.
There are two main distinctions between ordinary Turing machines and simple inductive Turing machines. The first distinction is that even simple inductive Turing machines can do much more than conventional Turing machines. The second distinction is that a conventional Turing machine will always determine (by coming to a final state) when the result is obtained, while a simple inductive Turing machine, in some cases (such as when "computing" something that cannot be computed by an ordinary Turing machine), will not be able to make this determination.
Schmidhuber's generalized Turing machines
A symbol sequence is computable in the limit if there is a finite, possibly non-halting program on a universal Turing machineUniversal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
that incrementally outputs every symbol of the sequence. This includes the dyadic expansion of π but still excludes most of the real numbers, because most cannot be described by a finite program. Traditional Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s cannot edit their previous outputs; generalized Turing machines, according to Jürgen Schmidhuber
Jürgen Schmidhuber
Jürgen Schmidhuber is a computer scientist and artist known for his work on machine learning, universal Artificial Intelligence , artificial neural networks, digital physics, and low-complexity art. His contributions also include generalizations of Kolmogorov complexity and the Speed Prior...
, can. He defines the constructively describable symbol sequences as those that have a finite, non-halting program running on a generalized Turing machine, such that any output symbol eventually converges, that is, it does not change any more after some finite initial time interval. Due to limitations first exhibited by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
(1931), it may be impossible to predict the convergence time itself by a halting program, otherwise the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
could be solved. Schmidhuber (2000, 2002) uses this approach to define the set of formally describable or constructively computable universes or constructive theories of everything
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
. Generalized Turing machines and simple inductive Turing machines are two classes of super-recursive algorithms that are the closest to recursive algorithms.
Relation to the Church–Turing thesis
The Church–Turing thesis in recursion theory relies on a particular definition of the term algorithm. Based on definitions that are more general than the one commonly used in recursion theory, Burgin argues that super-recursive algorithms, such as inductive Turing machines disprove the Church–Turing thesisChurch–Turing thesis
In computability theory, the Church–Turing thesis is a combined hypothesis about the nature of functions whose values are effectively calculable; in more modern terms, algorithmically computable...
. He proves furthermore that super-recursive algorithms could theoretically provide even greater efficiency gains than using quantum algorithms.
Burgin's interpretation of super-recursive algorithms has encountered opposition in the mathematical community. One critic is logician Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, who argues that Burgin's claims have been well understood "for decades". Davis states,
- "The present criticism is not about the mathematical discussion of these matters but only about the misleading claims regarding physical systems of the present and future."(Davis 2006: 128)
Davis disputes Burgin's claims that sets at level
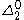of the arithmetical hierarchyArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
can be called computable, saying
- "It is generally understood that for a computational result to be useful one must be able to at least recognize that it is indeed the result sought." (Davis 2006: 128)
External links
- A New Paradigm for Computation. Los Angeles ACM Chapter Meeting, December 1, 1999.
- Anytime algorithm from FOLDOC