
Subliminal channels
Encyclopedia
In cryptography, subliminal channels are covert channels that can be used to communicate secretly in a normal looking communication over an insecure channel with help of digital signature
s. Subliminal channels in digital signature crypto systems were found in 1984 by Gustavus Simmons
.
Simmons describes how the dilemma can be solved through parameter substitution in digital signature
algorithms. In signature algorithms like ElGamal
and DSA
exist parameters which have to be set with random. He shows how one can make usage of these parameter to send a message subliminally. Because the algorithm's signature creation procedure is unchanged, the signature remains verifiable and indistinguishable from a normal signature. Therefore it is hard to detect if the subliminal channel is used.
Subliminal channels can be classified into broadband and narrow-band channel.
The broadband channel uses almost all available bits. Every channel which uses less bits is called a narrow-band channel. The additionally used bits are needed for further protection, e.g., impersonation.
The broadband and the narrow-band channels can use different algorithm parameters.
A narrow-band channel cannot transport maximal information, but it preserves the authentication key.
Further developments enhance the subliminal channel, e.g., allow for establishing a broadband channel without the need to agree on an authentication key in advance.
Other developments try to avoid the entire subliminal channel.
The question "Hello, how do you do?" would therefore send the subliminal message "1".
The Digital Signature Algorithm
has a subliminal broadband. and three subliminal narrow-band channels
At signing the parameter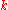 has to be set random. For the broadband channel this parameter is instead set with a subliminal message
has to be set random. For the broadband channel this parameter is instead set with a subliminal message  .
.
The formula for message extraction is derived by transposing the signature value calculation formula.
calculation formula.
The Newton channel is not a subliminal channel, but it can be viewed as an enhancement.
and the commitment scheme
it is possible to prevent the usage of the subliminal channel.
It should be mentioned that the countermeasure from has a 1-bit subliminal channel. The reason for that is the problem that a proof can succeed or purposely fail.
Another countermeasures can detect, not prevent, the subliminal usage of the randomness.
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s. Subliminal channels in digital signature crypto systems were found in 1984 by Gustavus Simmons
Gustavus Simmons
Gustavus J. Simmons is a retired cryptographer and former manager of the applied mathematics Department and Senior Fellow at Sandia National Laboratories...
.
Simmons describes how the dilemma can be solved through parameter substitution in digital signature
Digital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
algorithms. In signature algorithms like ElGamal
ElGamal signature scheme
The ElGamal signature scheme is a digital signature scheme which is based on the difficulty of computing discrete logarithms. It was described by Taher ElGamal in 1984....
and DSA
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
exist parameters which have to be set with random. He shows how one can make usage of these parameter to send a message subliminally. Because the algorithm's signature creation procedure is unchanged, the signature remains verifiable and indistinguishable from a normal signature. Therefore it is hard to detect if the subliminal channel is used.
Subliminal channels can be classified into broadband and narrow-band channel.
The broadband channel uses almost all available bits. Every channel which uses less bits is called a narrow-band channel. The additionally used bits are needed for further protection, e.g., impersonation.
The broadband and the narrow-band channels can use different algorithm parameters.
A narrow-band channel cannot transport maximal information, but it preserves the authentication key.
Further developments enhance the subliminal channel, e.g., allow for establishing a broadband channel without the need to agree on an authentication key in advance.
Other developments try to avoid the entire subliminal channel.
Examples
The easiest way to establish a subliminal channel is, to define that an even word count in a sentence is associated with the bit "0" and an odd word count with the bit "1".The question "Hello, how do you do?" would therefore send the subliminal message "1".
The Digital Signature Algorithm
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
has a subliminal broadband. and three subliminal narrow-band channels
At signing the parameter
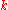 has to be set random. For the broadband channel this parameter is instead set with a subliminal message
has to be set random. For the broadband channel this parameter is instead set with a subliminal message  .
.- Key generation
- choose prime
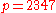
- choose prime

- calculate generator
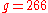
- choose authentication key
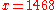 and send it securely to the receiver
and send it securely to the receiver - calculate public key
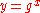 mod
mod 
- choose prime
- Signing
- choose message
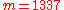
- (hash function
 is here substituted with a modulo reduction by 107) calculate message hash value
is here substituted with a modulo reduction by 107) calculate message hash value  mod
mod 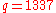 mod
mod 
- instead of random value
 subliminal message
subliminal message  is chosen
is chosen - calculate inverse of the subliminal message
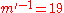 mod
mod 
- calculate signature value
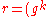 mod
mod  mod
mod 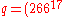 mod
mod 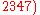 mod
mod 
- calculate signature value
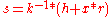 mod
mod  mod
mod 
- sending message with signature triple
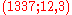
- choose message
- Verifying
- receiver gets message triple
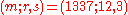
- calculate message hash
 mod
mod 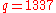 mod
mod 
- calculate inverse
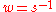 mod
mod 
- calculate
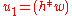 mod
mod  mod
mod 
- calculate
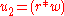 mod
mod 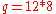 mod
mod 
- calculate signature
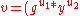 mod
mod 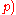 mod
mod 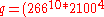 mod
mod 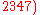 mod
mod 
- since
 , the is signature valid
, the is signature valid
- receiver gets message triple
- Message extraction on receiver side
- from triple (1337; 12, 3)
- extract message
 mod
mod 
The formula for message extraction is derived by transposing the signature value
 calculation formula.
calculation formula.
-
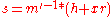 mod
mod 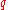
-
 mod
mod 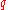
-
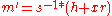 mod
mod 
Improvements
A modification to the Brickell and DeLaurentis signature scheme provides a broadband channel without the necessity to share the authentication key.The Newton channel is not a subliminal channel, but it can be viewed as an enhancement.
Countermeasures
With the help of the zero-knowledge proofZero-knowledge proof
In cryptography, a zero-knowledge proof or zero-knowledge protocol is an interactive method for one party to prove to another that a statement is true, without revealing anything other than the veracity of the statement....
and the commitment scheme
Commitment scheme
In cryptography, a commitment scheme allows one to commit to a value while keeping it hidden, with the ability to reveal the committed value later. Commitments are used to bind a party to a value so that they cannot adapt to other messages in order to gain some kind of inappropriate advantage...
it is possible to prevent the usage of the subliminal channel.
It should be mentioned that the countermeasure from has a 1-bit subliminal channel. The reason for that is the problem that a proof can succeed or purposely fail.
Another countermeasures can detect, not prevent, the subliminal usage of the randomness.

