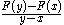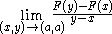Strictly differentiable
Encyclopedia
In mathematics
, strict differentiability is a modification of the usual notion of differentiability of functions
that is particularly suited to p-adic analysis
. In short, the definition is made more restrictive by allowing both points used in the difference quotient
to "move".
The function f:I→R is said strictly differentiable in a point a∈I if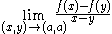
exists, where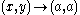
is to be considered as limit in 
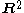, and of course requiring 
.
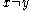A strictly differentiable function is obviously differentiable, but the converse is wrong, as can be seen from the counter-example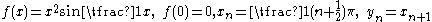
.
One has however the equivalence of strict differentiability on an interval I, and being of differentiability class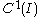
.
The previous definition can be generalized to the case where R is replaced by a normed vector space E, and requiring existence of a continuous linear map L such that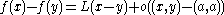
where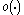
is defined in a natural way on E×E.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, strict differentiability is a modification of the usual notion of differentiability of functions
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
that is particularly suited to p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
. In short, the definition is made more restrictive by allowing both points used in the difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
to "move".
Basic definition
The simplest setting in which strict differentiability can be considered, is that of a real-valued function defined on an interval I of the real line.The function f:I→R is said strictly differentiable in a point a∈I if
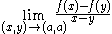
exists, where
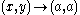is to be considered as limit in 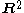, and of course requiring 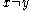.A strictly differentiable function is obviously differentiable, but the converse is wrong, as can be seen from the counter-example
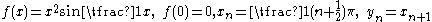.One has however the equivalence of strict differentiability on an interval I, and being of differentiability class
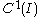.The previous definition can be generalized to the case where R is replaced by a normed vector space E, and requiring existence of a continuous linear map L such that
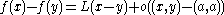
where
is defined in a natural way on E×E.Motivation from p-adic analysis
In the p-adic setting, the usual definition of the derivative fails to have certain desirable properties. For instance, it is possible for a function that is not locally constant to have zero derivative everywhere. An example of this is furnished by the function F: Zp → Zp, where Zp is the ring of p-adic integers, defined by-
One checks that the derivative of F, according to usual definition of the derivative, exists and is zero everywhere, including at x = 0. That is, for any x in Zp,
Nevertheless F fails to be locally constant at the origin.
The problem with this function is that the difference quotients
do not approach zero for x and y close to zero. For example, taking x = pn − p2n and y = pn, we have
which does not approach zero. The definition of strict differentiability avoids this problem by imposing a condition directly on the difference quotients.
Definition in p-adic case
Let K be a complete extension of Qp (for example K = Cp), and let X be a subset of K with no isolated points. Then a function F : X → K is said to be strictly differentiable at x = a if the limit
exists. -
