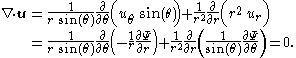
Stokes stream function
Encyclopedia

Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Stokes stream function is used to describe the streamlines and flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
in a three-dimensional incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
with axisymmetry. A surface with a constant value of the Stokes stream function encloses a streamtube, everywhere tangential to the flow velocity vectors. Further, the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
within this streamtube is constant, and all the streamlines of the flow are located on this surface. The velocity field associated with the Stokes stream function is solenoidal—it has zero divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
. This stream function is named in honor of George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
.
Cylindrical coordinates
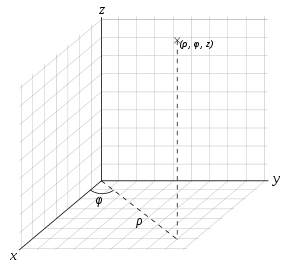
Cylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
( ρ , φ , z ), with the z–axis the line around which the incompressible flow is axisymmetrical, φ the azimuthal angle and ρ the distance to the z–axis. Then the flow velocity components uρ and uz can be expressed in terms of the Stokes stream function
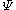 by:
by:
The azimuthal velocity component uφ does not depend on the stream function. Due to the axisymmetry, all three velocity components ( uρ , uφ , uz ) only depend on ρ and z and not on the azimuth φ.
The volume flux, through the surface bounded by a constant value ψ of the Stokes stream function, is equal to 2π ψ.
Spherical coordinates
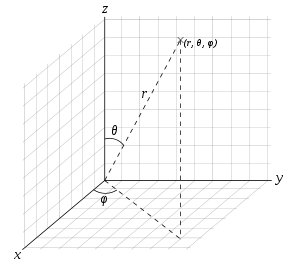
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
( r , θ , φ ), r is the radial distance from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, θ is the zenith angle
Zenith Angle
Zenith Angle can refer to:* In astronomy, the angle made between the surface of the Earth and a line between the observer and the observed * The Zenith Angle is a science fiction novel authored by Bruce Sterling...
and φ is the azimuthal angle. In axisymmetric flow, with θ = 0 the rotational symmetry axis, the quantities describing the flow are again independent of the azimuth φ. The flow velocity components ur and uθ are related to the Stokes stream function
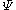 through:
through: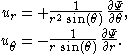
Again, the azimuthal velocity component uφ is not a function of the Stokes stream function ψ. The volume flux through a stream tube, bounded by a surface of constant ψ, equals 2π ψ, as before.
Vorticity
The vorticity is defined as: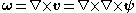 , where
, where 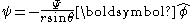 .
.
Derivation of vorticity  using a Stokes stream function using a Stokes stream function |
|---|
Consider the vorticity as defined by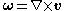 From the definition of the curl in spherical coordinates Del in cylindrical and spherical coordinates This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in... :  First we notice that the  and and  components are equal to 0. Secondly we substitute components are equal to 0. Secondly we substitute 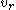 and and 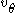 into into  then we get: then we get: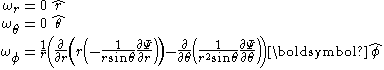 If we do the algebra:  |
If we do the calculation we find that the vorticity vector is equal to:
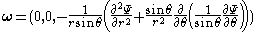
If we define the new operator
 then we have
then we have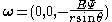
Comparison with cylindrical
The cylindrical and spherical coordinate systems are related through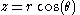 and
and 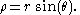
Zero divergence
In cylindrical coordinates, the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the velocity field u becomes:
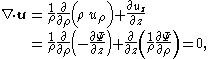
as expected for an incompressible flow.
And in spherical coordinates: