
Stokes' law (sound attenuation)
Encyclopedia
Stokes derived a law for the attenuation
of sound
in a Newtonian fluid
.
According to this law attenuation of sound α is proportional to the dynamic viscosity η, square of the sound frequency
ω, and reciprocally proportional to the fluid density
ρ and cubic power of sound speed V
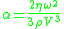
Attenuation is expressed in neper
per meter in this equation.
The author of this law is the same famous George Gabriel Stokes
who derived the well-known Stokes' law
for the friction force in fluids. It is 160 years old. This remarkable law does not contain unknown or unmeasurable parameters.
There has been substantial theoretical development in this field since Stokes’ pioneering work. It has brought one important correction to the Stokes law. It turns out that in addition to the dynamic viscosity the parameter of volume viscosity
ηv also affects the total attenuation according to the following relationship:
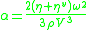
The parameter volume viscosity
is surprisingly little known despite its fundamental role for fluid dynamics
at high frequencies. This parameter appears in Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics , , and the acoustics , .
This volume viscosity coefficient becomes important only for such effects where fluid compressibility is essential and, importantly, ultrasound propagation is one such effect. Indeed, many rheological texts just assume the fluid to be incompressible and the volume viscosity therefore plays no role.
The only values for the volume viscosity of simple Newtonian fluids known to us come from the old Litovitz and Davis review . They report a volume viscosity of water at 15 Co equals 3.09 centipoise
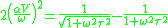
where relaxation time
τ equals:

Corresponding relaxation frequency is about 1000 GHz
. It is extremely high. For all practical purposes of describing sound attenuation in Newtonian fluids Stokes' law is clearly sufficient.
Attenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
of sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
in a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
.
According to this law attenuation of sound α is proportional to the dynamic viscosity η, square of the sound frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ω, and reciprocally proportional to the fluid density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
ρ and cubic power of sound speed V
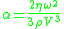
Attenuation is expressed in neper
Neper
The neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. It has the unit symbol Np. The unit's name is derived from the name of John Napier, the inventor of logarithms...
per meter in this equation.
The author of this law is the same famous George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
who derived the well-known Stokes' law
Stokes' law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
for the friction force in fluids. It is 160 years old. This remarkable law does not contain unknown or unmeasurable parameters.
- It is convenient to convert attenuation into other units, by normalizing attenuation with respect to frequency, because the attenuation typically increases rapidly with frequency. These new units make more adequate presentation of attenuation within a wide frequency range. It is seen that attenuation of the Newtonian fluid, presented in these units, becomes a linear function of frequency.
There has been substantial theoretical development in this field since Stokes’ pioneering work. It has brought one important correction to the Stokes law. It turns out that in addition to the dynamic viscosity the parameter of volume viscosity
Volume viscosity
Volume viscosity becomes important only for such effects where fluid compressibility is essential. Examples would include shock waves and sound propagation...
ηv also affects the total attenuation according to the following relationship:
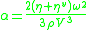
The parameter volume viscosity
Volume viscosity
Volume viscosity becomes important only for such effects where fluid compressibility is essential. Examples would include shock waves and sound propagation...
is surprisingly little known despite its fundamental role for fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
at high frequencies. This parameter appears in Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics , , and the acoustics , .
This volume viscosity coefficient becomes important only for such effects where fluid compressibility is essential and, importantly, ultrasound propagation is one such effect. Indeed, many rheological texts just assume the fluid to be incompressible and the volume viscosity therefore plays no role.
The only values for the volume viscosity of simple Newtonian fluids known to us come from the old Litovitz and Davis review . They report a volume viscosity of water at 15 Co equals 3.09 centipoise
- More recent studies have established that Stokes's law is actually a low frequency asymptotic of the more general relationship that describes sound attenuation at very high frequencies:
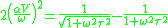
where relaxation time
Relaxation time
In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium.Each relaxation process can be characterized by a relaxation time τ...
τ equals:

Corresponding relaxation frequency is about 1000 GHz
GHZ
GHZ or GHz may refer to:# Gigahertz .# Greenberger-Horne-Zeilinger state — a quantum entanglement of three particles.# Galactic Habitable Zone — the region of a galaxy that is favorable to the formation of life....
. It is extremely high. For all practical purposes of describing sound attenuation in Newtonian fluids Stokes' law is clearly sufficient.

